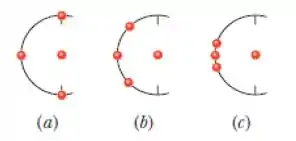
A figura mostra três arranjos das mesmas partículas idênticas, com três delas colocadas sobre um arco de circunferência de raio , e a quarta colocada no centro do arco. Ordene os arranjos de acordo com o módulo da força gravitacional resultante que age sobre a partícula central devido às outras três partículas, começando pela maior.
(a) c, b, a;
(b) c, a, b;
(c) b, c, a;
(d) b, a, c;
(e) c, depois a e b empatados;
Passo 1
Vamos analisar a força gravitacional sobre a partícula central.
As três partículas sobre o arco exercem exatamente a mesma força gravitacional em módulo sobre a partícula central. Isso porque tanto as distâncias quanto as massas são iguais.
Porém, o que muda de um arranjo para o outro é a direção de cada força.
Passo 2
Em todos os arranjos, a partícula alinhada horizontalmente vai estar na mesma posição e vai exercer uma força na mesma direção:
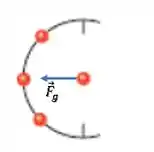
Já a partícula de baixo e de cima vão variar seu afastamento com relação à primeira.
Vamos escrever a força de acordo com um ângulo com a horizontal:
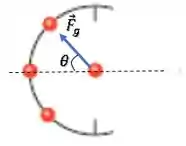
Decompondo a força , temos:
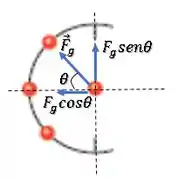
Porém, a partícula de baixo terá um arranjo de força bem parecido, porém, com sua componente vertical para baixo:
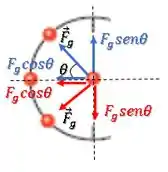
Logo, as componentes na vertical se cancelam.
A força resultante para os três arranjos diferentes vai depender apenas das componentes da força na horizontal:
Tanto pela figura quanto pela expressão, percebemos que quanto menor o ângulo de inclinação , maior serão as componentes horizontais , portanto maior será a força resultante .
Então, descobrimos que a força resultante será maior em (c), pois as componentes na vertical são menores (se cancelam) e as componentes na horizontal são maiores (se somam). O arranjo (b) terá a segunda maior força resultante em módulo, seguida pelo arranjo (a).
Ficamos com a letra (a) -> c,b,a
Resposta
Letra (a)