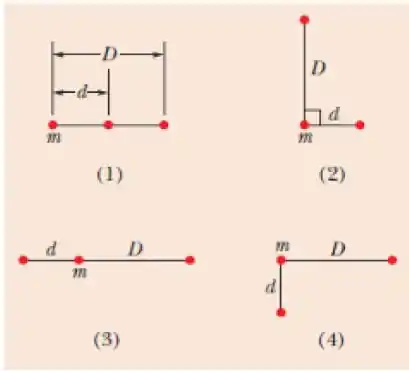
A figura mostra quatro arranjos de três partículas de massas iguais. Ordene os arranjos de acordo com o módulo da força gravitacional resultante sobre a partícula identificada por , começando pela maior
(a) 1, depois 2 e 4 empatados, 3
(b) 1, 2, 3, 4
(c) 1 e 2 empatados, 3, 4
(d) 2 e 4 empatados, 1, 3
(e) 4, 3, 2, 1
Passo 1
Vamos ver como é a força gravitacional em cada arranjo.
No arranjo as forças exercidas pelas outras partículas apontam pra direita e se somam
Passo 2
No arranjo as duas forças são ortogonais entre si, então para obter a força resultante temos que fazer Pitágoras
Passo 3
No arranjo as duas forças apontam em sentidos opostos, nesse caso temos que subtrair as duas
Passo 4
O arranjo é igual ao arranjo só que rotacionado, assim
Passo 5
A maior vai ser o caso em que as duas se somam direto, ou seja, o caso , enquanto que o caso vai ser o caso em que a resultante vai ser a menor possível já que as duas foras se subtraem. O caso em que as duas são ortogonais vai ser o caso intermediário. Assim
Assim a resposta vai ser o item (a)
Resposta
(a)