Uma esfera de chumbo de raio possui uma cavidade esférica cuja superfície passa pelo centro da esfera e “toca” o lado direito da esfera. A massa da esfera, antes de a cavidade ser aberta, era . Com que força gravitacional a esfera de chumbo com a cavidade atrai uma pequena esfera de massa que se encontra a uma distância do centro da esfera de chumbo, sobre a reta que liga os centros da esfera e da cavidade?
.
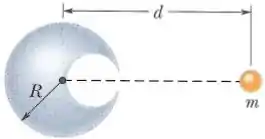
Passo 1
Vamos primeiramente calcular a força que a esfera de chumbo faz na esfera menor, sem ter a cavidade.
Passo 2
Agora vamos imaginar a cavidade como sendo uma esfera de raio , cujo o centro de massa está a uma distância de da esfera pequena. Agora vamos calcular a força gravitacional que essa cavidade esférica exerceria na esfera pequena.
Entretanto, não temos a massa dessa cavidade esférica. Mas podemos descobrir utilizando a fórmula da densidade:
Para a esfera sem a cavidade, temos que e o volume será:
Logo, substituindo:
Agora é só utilizar a densidade para a cavidade:
Entretanto, ainda temos que calcular o volume da cavidade. Mas sabemos que o raio da cavidade é a metade do raio da esfera, ou seja, é .
Substituindo na fórmula:
Agora é só substituir na fórmula
Passo 3
Agora para calcular a força que a esfera com a cavidade faz, é só diminuir as duas forças: