A que distância de uma esfera de e raio uma partícula teria de ser posta para que a esfera atraísse a partícula com a mesma força com que a Terra atrai esta partícula posta na sua superfície? Esse experimento poderia ser efetivamente realizado?
Dados:
Raio da Terra:
Massa da Terra:
Passo 1
Primeiro vamos calcular a intensidade da força que a Terra atrai a partícula na sua superfície.
A força gravitacional é dada por:
A massa será a massa da Terra , a distância será a distância do centro da Terra até sua superfície, portanto será o raio da Terra e é a massa da partícula:
Ahh beleza, essa é a força que a Terra exerce sobre a partícula em sua superfície, mas vamos à pergunta...
Passo 2
Imagina essa partícula perto de uma esfera de :
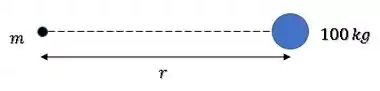
A esfera vai exercer uma força gravitacional sobre a partícula:
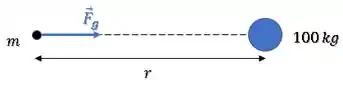
Essa força vai ser dada por:
Onde é a massa da esfera, a massa da partícula e a distância entre eles.
Queremos encontrar a distância que faz essa força gravitacional ser igual à força que a Terra exerce sobre a partícula.
Passo 3
Vamos igualar a expressão da força que a esfera exerce sobre a partícula com a expressão da força que a Terra exerce sobre a partícula :
Cortando a massa e a constante :
Isolando , temos:
Fazendo essas contas, temos que:
Então, a distância que a partícula deve estar do centro da esfera é:
Passo 4
Além de simplesmente encontrar a distância , devemos interpretar esse resultado e responder se isso é possível.
Bom, vamos pensar na situação:

Sabemos que é bem pequeno, então, a partícula deve estar bem próxima da esfera.
Mas dá uma olhada no raio da esfera:
Se a gente passar a distância para centímetros, fica bem fácil de ver que:
A distância na qual a partícula deveria estar do centro da esfera é muitooooo menor que o próprio raio da esfera:
Como não tem como a partícula se aproximar a uma distância menor que , o experimento é impossível.
Resposta
Distância:
O experimento é impossível de ser realizado, pois a distância é menor que o próprio raio da esfera .