Uma massa pontual de e outra de são mantidas fixas a de distância. Uma partícula de massa é solta de um ponto entre as duas massas a da massa de ao longo da linha que une as duas massas fixas. Qual o módulo, a direção e o sentido da aceleração da partícula imediatamente após ser solta?
Dados:
Passo 1
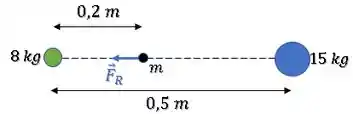
A situação é a seguinte:
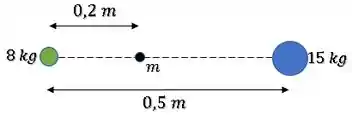
Uma partícula de massa foi solta no meio de duas outras partículas de massas e .
Cada uma delas vai exercer uma força gravitacional sobre a partícula de massa :
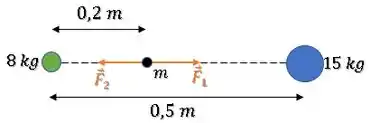
Queremos saber o módulo, a direção e o sentido da aceleração da partícula de massa .
Para isso, vamos calcular cada uma das duas forças gravitacionais e descobrir a força resultante agindo sobre a partícula. Feito isso, podemos descobrir a aceleração a partir da segunda lei de Newton:
Passo 2
A força gravitacional é dada por:
Onde é a constante gravitacional, e são as massas das partículas e é a distância entre elas.
A força será a força gravitacional entre a partícula de massa e a partícula de massa igual a :
Mas qual é a distância entre elas?
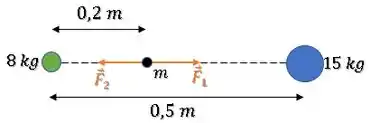
A distância será:
Então, temos:
Enquanto a força gravitacional será entre a partícula de massa e a partícula de massa igual a :
Passo 3
A força resultante será:
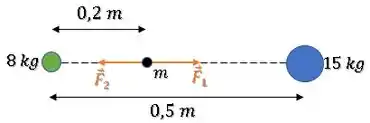
Agora, podemos escolher qualquer referencial. Vamos considerar o sentido para a esquerda como positivo, então:
Então, a força resultante está para a esquerda na direção de :
A aceleração vai apontar na mesma direção da força, portanto, na direção da partícula de .
Passo 4
Agora, vamos aplicar a segunda lei de Newton e descobrir a aceleração :
Substituindo o valor da constante gravitacional , temos:
Resposta
A aceleração aponta na direção da partícula de .