Imagine o sistema composto pelo planeta Terra de massa e pela Lua com massa . Seja ainda a distância entre a Terra e a Lua dada por . A que distância da Terra sobre a reta que une os dois corpos a força gravitacional sobre uma partícula ali situada será zero?
(A)
(B)
(C)
(D)
(E)
Passo 1
Se uma partícula está entre a Terra e a Lua, ela sofre uma força gravitacional para cada lado:
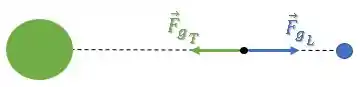
Se a força gravitacional resultante é zero:
Passo 2
A distância da partícula a cada um dos corpos é:
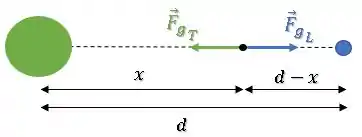
Vamos chamar a massa da pratícula de :
Podemos cortar e .
Parabéns pela bela participação, “”.
Além disso, sabemos que a massa da Lua é:
Tirando a raiz quadrada dos dois lados, temos:
Ficamos com a letra (D).
Resposta
Letra (D)
Exercícios de Livros Relacionados
As massas e coordenadas de três esferas são as seguintes: 20k g , x = 0,50m , y = 1,0m ; 40k g , x = - 1,0m , y = - 1,0m ; 60k g , x = 0m , y =- 0,50m . Qual é o módulo da força gravitacional que as t
Qual deve ser a distância entre uma partícula de 5,2 kg e uma partícula de 2,4 kg para que a atração gravitacional entre elas tenha um módulo de 2,3 × 10 - 12 N ?
Miniburacos negros. Talvez existam miniburacos negros no universo, produzidos logo após o big bang. Se um desses objetos, com massa de 1 × 10 11 k g (e um raio de apenas 1 × 10 - 16 m ) se aproximasse
Na Fig. 13-33, três esferas de 5,00 kg estão localizadas a distâncias de d 1 = 0,300 m e d 2 = 0,400 m . Qual é (a) o módulo e (b) a orientação (em relação ao semieixo x positivo) da força gravitacion
Nos Problemas de 65 a 68, você recebe a(s) equação(ções) usada(s) para solucionar cada problema. Em cada caso, você deve: a. Redigir um problema realista para o qual esta seja a equação correta. b. Fa