Uma partícula pontual de massa está sobre o eixo em e uma partícula idêntica está sobre o eixo em . (a) Qual é a orientação do campo gravitacional da origem? (b) Qual é a magnitude deste campo?
Passo 1
A gente precisa calcular o campo gravitacional aqui, já que o problema nos pede a orientação e a magnitude dele em relação a origem O, na nossa língua quer dizer que ele quer o valor do campo e pra onde ele aponta. Temos duas partículas idênticas que tem a mesma distância da origem.
Vamos desenhar o problema:
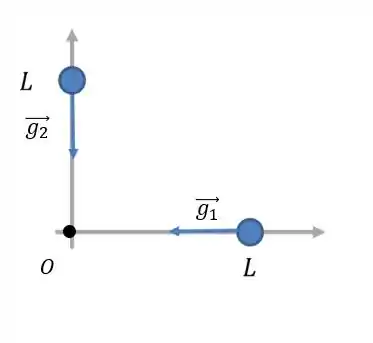
Repara que a gravidade pra cada uma das partículas aponta pra um sentido diferente. O campo gravitacional depende da massa e também da distância quanto mais distante menor é a influencia do campo e nesse caso todas as componentes são iguais pra cada partícula. Vetorialmente falando a fórmula que descreve o campo gravitacional é essa aqui:
Passo 2
Quando ele fala em orientação a gente pode pensar em duas coisas, na orientação vetorial ou no ângulo da resultante desse campo. A gente viu como funciona na fórmula e só vamos precisar ali mudar o sentido, que é negativo.
E pra encontrar o ângulo dessa resultante a gente pode desenhar a resultante dos vetores e calcular a tangente do triângulo.
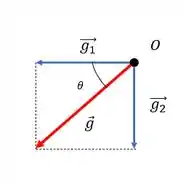
Que vai ser dada por cada módulo aqui, já que os vetores ortogonais possuem só uma direção:
E aí a gente faz a inversa:
Passo 3
E o módulo do vetor é só fazer o Pitágoras daquele mesmo triângulo com as compontenes em módulo, se liga:
Substituindo geral a gente tem: