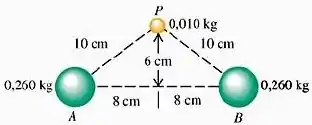
Duas esferas uniformes, cada uma com massa igual a , estão fixas nos pontos e . Determine o módulo, a direção e o sentido da aceleração inicial de uma esfera uniforme com massa quando ela é liberada do repouso no ponto e sofrendo apenas atrações gravitacionais das esferas situadas em e .
Passo 1
A massa da esfera que está no ponto não vai interferir, porque? Lembra que a aceleração da gravidade é
Basta assumirmos sendo a distância entre as esferas, e sendo a massa da esfera verde e pronto temos as acelerações do ponto . Pois bem, assumiremos os valores:
Como os corpos tem a mesma massa a intensidade da gravidade é igual, vamos calcular?
Passo 2
As acelerações vão ser assim
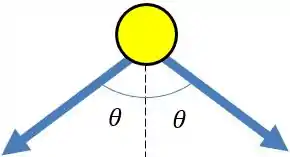
Repara que os ângulos são iguais porque os triângulos são iguais. Como as acelerações são iguais vamos ter apenas componente vertical, ambas apontando para baixo. Usando a “regra do COlado/SEparado” vamos ter
Mas quem é cosseno de ? Olha no triângulo da figura inicial, o cosseno não é cateto adjacente sobre hipotenusa? Então
Vamos ter
Passo 3
Essa é a COMPONENTE de cada gravidade a aceleração total vai ser