Listas de Cálculo 1 - UERJ de Cálculo I da UERJ - Lista 8
Determine o número de raízes reais distintas que o polinômio
possui.
Dica: Use o Teorema do valor médio para mostrar que possui no máximo raízes reais distintas e em seguida o Teorema do Valor Intermediário para garantir a existência delas.
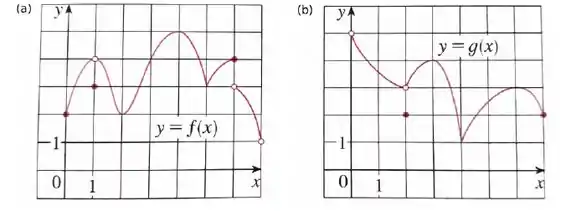
Ver solução completaUse os gráficos abaixo para dizer quais são os pontos e os valores de máximo e mínimo locais e globais da função.
Em cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(a)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(b)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(c)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(d)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(e)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(f)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(g)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(h)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(i)
Ver solução completaEm cada item a seguir, encontre os pontos críticos da função dada (caso existirem).
(j)
Ver solução completaEm cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(a) ,
Ver solução completaEm cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(b) ,
Ver solução completaEm cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(c) ,
Ver solução completaEm cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(d) ,
Ver solução completaEm cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(e) ,
Ver solução completaEm cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(f) ,
Ver solução completaEm cada item a seguir, determine os valores máximo e mínimo globais da função dada no intervalo dado.
(g) ,
Ver solução completaApós o consumo de uma bebida alcoólica, a concentração de álcool no sangue (CAS) aumenta rapidamente à medida que o álcool é absorvido, seguida por uma diminuição gradual conforme o álcool é metabolizado pelo fígado. A função
modela a CAS média, medida em mg/mL, de um grupo de oito indivíduos do sexo masculino horas depois do consumo rápido de de etanol (correspondendo a uma dose de bebida alcoólica). Qual é a CAS média máxima durantes as primeiras horas? Quando ela ocorre?
Ver solução completaEm cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(a)
Ver solução completaEm cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(b)
Ver solução completaEm cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(c)
Ver solução completaEm cada item a seguir, encontre os intervalos de crescimento e decrescimento da função dada. Em seguida, determine seus pontos de máximo e mínimo locais (se existirem).
(d)
Ver solução completaEm cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(a)
Ver solução completaEm cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(b)
Ver solução completaEm cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(c)
Ver solução completaEm cada item a seguir, determine os intervalos em que tem concavidade voltada para cima e concavidade voltada para baixo. Em seguida, encontre seus pontos de inflexão.
(d)
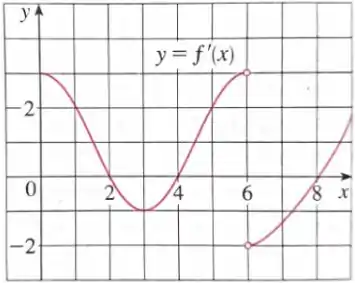
Ver solução completaO gráfico da função derivada de uma função contínua é dado abaixo
- Em que intervalos está crescendo? E decrescendo?
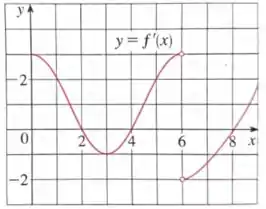
O gráfico da função derivada de uma função contínua é dado abaixo
- Em quais pontos a função tem um máximo local? E em quais um mínimo local?
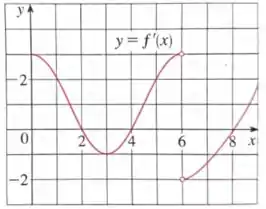
O gráfico da função derivada de uma função contínua é dado abaixo
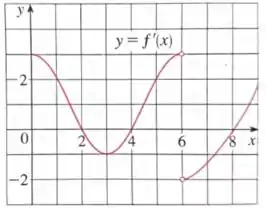
- Em que intervalos tem concavidade voltada para cima? E concavidade voltada para baixo?
O gráfico da função derivada de uma função contínua é dado abaixo
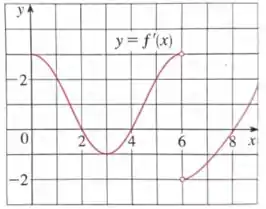
- Quais são os pontos de inflexão?
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
b)
Ver solução completaPara cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
Para cada função definida abaixo faça todos os itens a seguir:
- Encontre a função e os intervalos de crescimento e decrescimento de ;
- Encontre a função e estude a concavidade de .
A taxa aeróbica de uma pessoa com anos de idade pode ser modelada pela seguinte função:
Quando . Em que idade uma pessoa tem capacidade aeróbica máxima?
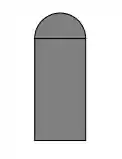
Ver solução completaUma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. Se o perímetro da janela for , encontre as dimensões da janela que deixam passar a maior quantidade possível de luz.
Mostre que dentre todos os retângulos com o mesmo perímetro, aquele com a maior área é um quadrado.
Ver solução completaEm cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
c)
para e para ,
para e para .
para ,
para e para .
Ver solução completaEm cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
(d) para todo ,
é uma assíntota vertical,
para e para ,
para
Ver solução completaUm contêiner para estocagem, retangular sem tampa, deve ter um volume de 10 m³. O comprimento de sua base é o dobro da sua largura. O material para a base
custa R$ 2,50 por metro quadrado. O material para os lados custa R$ 9,00 por metro quadrado. Encontre o valor y da largura do contêiner para que o custo da sua
construção seja o menor possível.
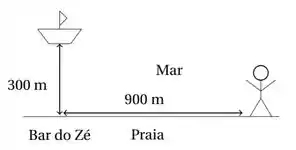
Um triatleta se encontra numa praia reta, a 900 m do Bar do Zé, quando vê uma criança cair de um barco no mar a 300 m da praia, na altura deste bar, como ilustrado abaixo. Se o atleta corre na areia a 500 m/min e nada a 400 m/min, determine o caminho que ele deve escolher para chegar o mais rápido possível ao resgate da criança. Quanto tempo vai demorar para percorrer este caminho? (Obs:300² + 400² = 500²).
Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
para todo .
para todo .
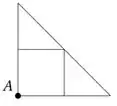
Ver solução completaConsidere retângulos inscritos em um triângulo retângulo com os dois lados do retângulo sobre os catetos do triângulo e o vértice A em comum. Determine as medidas do retângulo de maior área que pode ser inscrito em um triângulo retângulo com catetos de comprimentos 3 cm e 4 cm. Qual a área do retângulo encontrado? (Dica: use semelhança de triângulos para montar a função a ser otimizada).
O gráfico da função derivada f′ de uma função contínua f é dado abaixo.
e) Supondo que f (0) = 0, esboce o gráfico de f