UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 9c
Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
c)
para e para ,
para e para .
para ,
para e para .
Passo 1
Olá meu amigo, Yuri aqui e vamos dar continuidade a nossa criação de gráficos para derivadas de funções. As restrições aumentaram em relação a nossa ultima letra. Vamos analisar com calma cada uma delas para que possamos encontrar a nossa função desejada.
Se então f possui retas tangentes horizontais em e . Como se ou então f é crescente para valores de x menores que zero ou entre 2 e 4. Como se ou , então f é decrescente para valores de x maiores que 4 ou entre 0 e 2.
Passo 2
Como se então f possui concavidade voltada para cima para valores de x entre 1 e 3. E como se ou então f possui concavidade voltada para baixo para valores de x menores que 1 ou maiores que 3. Dito tudo isso, nosso gráfico é
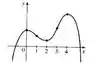
Resposta
Ver o desenvolvimento