UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 8b
O gráfico da função derivada de uma função contínua é dado abaixo
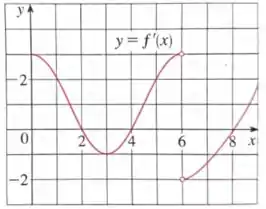
- Em quais pontos a função tem um máximo local? E em quais um mínimo local?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um gráfico de uma função derivada de uma função contínua :
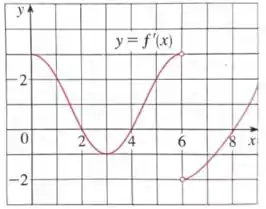
Queremos saber em quais pontos a função tem um máximo local e em quais um mínimo local.
Para isso, devemos saber de duas coisinhas:
- Se passa de positivo para negativo, então temos um máximo local naquele ponto;
- Se passa de negativo para positivo, então temos um mínimo local naquele ponto.
Eaí? Bora lá resolver?
😉
Passo 2
Então... se observarmos o gráfico, teremos os seguintes pontos que cruzam o eixo das abcissas:
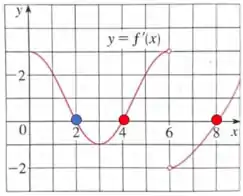
Dessa forma, temos um máximo local no ponto azul e mínimos locais nos pontos destacados em vermelho e .
Entendeu direitinho? Responde aee ;)
Resposta
Máximo local em
Mínimos locais em e
Exercícios de Livros Relacionados
O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)