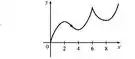
O gráfico da função derivada f′ de uma função contínua f é dado abaixo.
e) Supondo que f (0) = 0, esboce o gráfico de f
Passo 1
Olá meu amigo, como vai? Yuri aqui e agora vamos em busca do gráfico de a partir do gráfico de sua derivada. É importante que voce tenha acompanhado bem atentamente todo o desenvolvimento do que foi feito nas letras anteriores a essa para que finalmente possamos encontrar o gráfico de
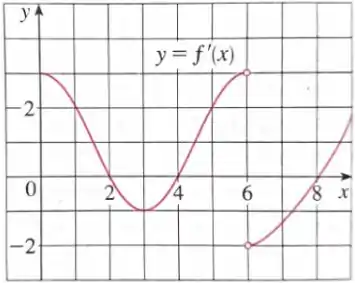
- O sinal da derivada indica se a função está crescendo (derivada positiva) ou decrescendo (derivada negativa). Podemos observar no gráfico que nos intervalos (0,2), (4,6) e temos e nos intervalos (2,4) e (6,8) , então:
- f é crescente nos intervalos (0,2), (4,6) e e decrescente nos intervalos (2,4) e (6,8)
- Se passa de positiva para negativa temos um máximo local e se passa de negativo para positivo temos um mínimo local. Então, temos máximo local em e e temos mínimo local em e .
- A concavidade de uma função é dada pelo sinal da derivada segunda. Se a derivada segunda for negativa, a concavidade da função é voltada para baixo e se for positiva a concavidade é voltada para cima. Como a derivada segunda aponta o crescimento e decrescimento da derivada primeira, então quando a derivada segunda for negativa, a derivada primeira será decrescente e caso seja positiva, a derivara primeira será crescente. Portando, podemos ver pelo gráfico que é crescente nos intervalos e e é decrescente no intervalo então:
- f possui concavidade para cima nos intervalos e e concavidade para baixo no intervalo .
- Os pontos de inflexão são aqueles em que a segunda derivada é nula, ou seja, a concavidade muda de sinal,
- O único ponto de inflexão é
Passo 2
Se , o gráfico de f passa pela origem, então de acordo com as informações levantas nos itens de 1) a 4), temos o seguinte gráfico.
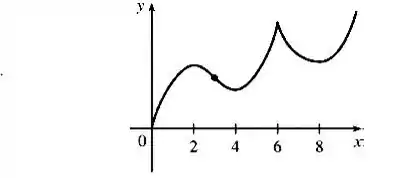
Resposta