UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 18
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. Se o perímetro da janela for , encontre as dimensões da janela que deixam passar a maior quantidade possível de luz.
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que calculemos as dimensões da janela de tal forma que seu perímetro deve ser de e passe a maior quantidade possível de luz (ou seja, maior área possível).
Bom... com as informações do enunciado, temos a seguinte representação:
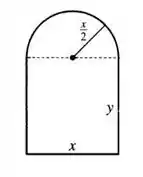
E aí, bora lá??
😉
Passo 2
Então... queremos a maior área possível.
A área é dada por:
A questão nos disse que o perímetro deve ser de , portanto:
Substituindo em , temos:
Passo 3
Maximizando , obtemos:
Substituindo em :
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Encontre a área do maior retângulo que pode ser inscrito na elipse x 2 a 2 + y 2 b 2 = 1
Um modelo usado para a produção Y de uma colheita agrícola como função do nível de nitrogênio N no solo (medido em unidades apropriadas) é Y = k N 1 + N 2 Em que k é um constante positiva. Que nível d
Gerentes de lojas querem uma política de estoque ótima. Excesso de estoque resulta em armazenagem excessiva e custos de estoque, enquanto que um estoque pequeno significa adicionar custo à reorganizaç
Um cilindro circular reto é inscrito em uma esfera de raio r . Encontre o maior volume possível para este cilindro.
Um cilindro circular reto é inscrito em um cone com altura h e raio da base r . Encontre o maior volume possível para este cilindro.