UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 11i
Esboce os gráficos das funções dadas a seguir:
i)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma função e nos pede esboçar o seu gráfico.
Para isso, temos que determinar o domínio da função, encontrar as intersecções nos eixos, assíntotas, intervalos de crescimento e decrescimento, máximos e mínimos, entre várias coisas.
Assim, vamos determinar uma característica dessas em cada passo, combinadinho?
Agora vamos lá!!
😉
Passo 2
Então... vamos verificar primeiro o domínio da função.
Para isso, precisamos considerar os valores de para os quais a função está definida.
Vemos que o denominador não pode ser . No entanto, como está elevado ao quadrado, não corre risco desse valor ser negativo.
Assim, o domínio são todos os números reais.
Passo 3
Para encontrarmos a intersecção como eixo , fazemos :
Para encontrarmos a intersecção como eixo , fazemos :
Passo 4
Para verificarmos se tem simetria, temos que saber que:
- Simetria Par: Uma função é simétrica em relação ao eixo se para todo no domínio de , tivermos ;
- Simetria Ímpar: Uma função é simétrica em relação ao eixo se para todo no domínio de , tivermos .
Fazendo , temos:
Logo, vemos que tem simetria par.
Passo 5
As assíntotas verticais ocorrem quando o denominador se anula. Neste caso, o denominador nunca se anula, portanto, não existem assíntotas verticais.
Ao analisar o comportamento de , vemos que:
E
Assim, é uma assíntota horizontal.
Passo 6
Para verificar os intervalos de crescimento e decrescimento da função, vamos derivar a função e depois igualar a zero.
Assim, observamos que:
Passo 7
Pelo passo 6, vimos que é um ponto crítico. Assim, substituindo em , temos:
Assim, baseado no crescimento e decrescimento da função, vemos que o ponto é um ponto de mínimo.
Passo 8
Com base nessas informações, podemos plotar o gráfico:
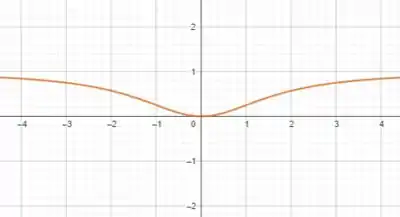
Entendeu direitinho? Responde aee ;)
Resposta
