UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 2
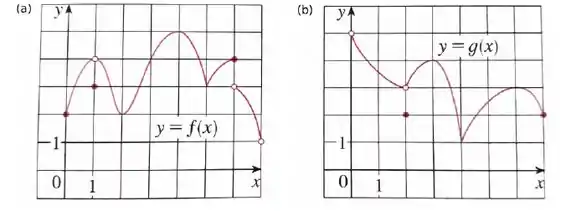
Use os gráficos abaixo para dizer quais são os pontos e os valores de máximo e mínimo locais e globais da função.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente verificar nos gráficos quais são os pontos de máximo e mínimo locais e globais da função.
Relembrando: um ponto de máximo é um ponto na função que é maior que os pontos próximos a ele e um ponto de mínimo é um ponto que é menor que os pontos próximos a ele. Quando é máximo global, ele é maior que todos os pontos da função e quando é mínimo global, ele é menor que todos os outros.
Al��m disso, tanto os pontos de máximo quanto os de mínimo tem uma reta tangente horizontal, isso significa que o coeficiente angular dessas retas é zero e que a derivada da função no ponto também é zero.
Basicamente, é isso que nós vamos identificar nos gráficos.
Vamos lá!
Passo 2
Vamos começar analisando o gráfico da figura da letra (a):
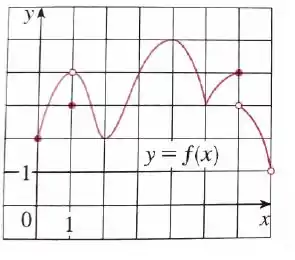
Observe que os pontos , e são menores que os valores nas suas vizinhanças. A gente não considera as bolinhas abertas, porque a função não tá definida nesses pontos. Então, temos os pontos de mínimo local em:
Agora repare que em e temos pontos maiores que em suas vizinhanças, que são picos da função. Esses picos são nossos pontos de máximo local:
E o maior de todos acontece em , que é também nosso máximo global (ou absoluto). Mas a função não tem mínimo global, como a gente observa ali no gráfico.
Passo 3
Agora vamos analisar o gráfico da letra (b):
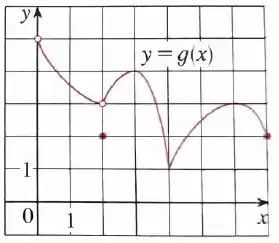
Da mesma forma que analisamos na letra (a), a gente consegue perceber que temos pontos de mínimo local em:
Além disso, observando os picos da nossa curva, temos nossos pontos de máximo local em:
E temos um ponto de mínimo absoluto em , mas a função não possui máximo absoluto. Não confunda com os pontos de bolinha aberta, hein? Nossa função não tá definida naqueles valores.
Valeu, galera! Até a próxima! 😉
Resposta
(a)
Mínimo local:
Mínimo global:
Máximo local:
Máximo global:
(b)
Mínimo local:
Mínimo global:
Máximo local:
Máximo global: