Um contêiner para estocagem, retangular sem tampa, deve ter um volume de 10 m³. O comprimento de sua base é o dobro da sua largura. O material para a base
custa R$ 2,50 por metro quadrado. O material para os lados custa R$ 9,00 por metro quadrado. Encontre o valor y da largura do contêiner para que o custo da sua
construção seja o menor possível.
Passo 1
Olá amigo, Yuri aqui e agora iremos resolver esse problema de otimização. O nosso contêiner com as suas respectivas variáveis é dado por
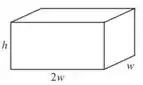
Sabemos que o volume do container é
E agora iremos calcular o custo total do contêiner, que é a soma dos custos da base com o da área lateral,
Passo 2
Do volume, podemos escrever
substituindo no custo, ficamos com
Como iremos encontrar o mínimo, é simples meu caro amigo, iremos derivar o custo e igualar a zero