Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
(d) para todo ,
é uma assíntota vertical,
para e para ,
para
Passo 1
Para encontrar uma função que satisfaça todas as condições dadas, você pode construir uma função composta de várias partes que atendam a cada uma das condições específicas. Vou guiá-lo através desse processo passo a passo:
Condição 1: f'(x) > 0 para todo x ≠ 1
Para atender a essa condição, podemos usar uma função crescente em todo o domínio, exceto em x = 1.
Condição 2: x = 1 é uma assíntota vertical
Uma assíntota vertical significa que a função se aproxima infinitamente de um valor específico à medida que x se aproxima de 1.
Condição 3: f''(x) > 0 para x 3
Para essa parte da condição, podemos usar uma função côncava para cima em x 3.
Condição 4: f''(x)
Para essa parte da condição, podemos usar uma função côncava para baixo em 1
Passo 2
Agora, podemos combinar todas essas partes em uma única função que satisfaça todas as condições, temos o gráfico:
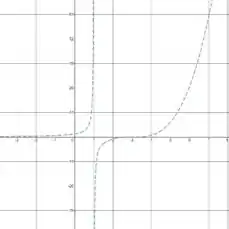
Resposta
Ver o desenvolvimento