UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 9b
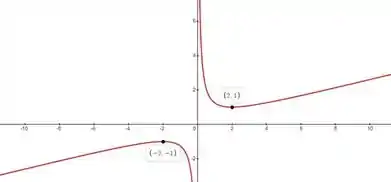
Em cada item a seguir, esboce o gráfico de uma função f que satisfaz a todas as condições dadas.
b) é uma assíntota vertical, para para , para .
Passo 1
Olá meu amigo, Yuri aqui e agora é hora de continuarmos desenhando nossos gráficos. Para esboçar o gráfico de uma função que satisfaça todas as condições dadas, podemos seguir estas etapas:
- x = 0 é uma assíntota vertical: Isso significa que a função deve se aproximar de infinito positivo ou negativo à medida que x se aproxima de 0. Podemos fazer isso adicionando uma assíntota vertical em x = 0.
- Para . Isso significa que f será crescente para . Para se . Significa que f será decrescente para
- f''(x) 0 para x > 0: Isso indica que a concavidade da função deve ser voltada para baixo à esquerda de x = 0 (côncava para baixo) e voltada para cima à direita de x = 0 (côncava para cima).
Passo 2
O grafico então para a função com essas caracteristicas é
Resposta
Ver o desenvolvimento
Exercícios de Livros Relacionados
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = e x
Seja f x = x 2 .(a) Estime os valores de f ' ( 0 ) , f ' 1 2 , f ' ( 1 ) e f ' ( 2 ) fazendo uso de uma ferramenta gráfica para dar zoom no gráfico de f .(b) Use a simetria para deduzir os valores de
Faça um esboço cuidadoso de f e abaixo dele esboce o gráfico de f ’ como foi feito nos Exercícios 4 - 11 . Você pode sugerir uma fórmula para f ‘ ( x ) a partir de seu gráfico? f x = s e n x
Trace o gráfico da função f x = { x 2,- 1 ≤ x0 - x 2 ,0 ≤ x ≤ 1 f é contínua em x=0 ? f é derivável em x=0 ?
Esboce o gráfico de f à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de f . f x = x 2 ,- 3 ≤ x ≤ 2