UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 8c
O gráfico da função derivada de uma função contínua é dado abaixo
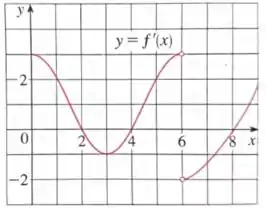
- Em que intervalos tem concavidade voltada para cima? E concavidade voltada para baixo?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um gráfico de uma função derivada de uma função contínua :
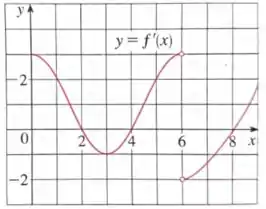
Queremos saber em que intervalos tem concavidade voltada para cima e concavidade voltada para baixo.
Para isso, temos que saber que a concavidade de uma função é dada pelo sinal da derivada segunda.
Eaí? Bora lá resolver?
😉
Passo 2
Então... Se a derivada segunda for negativa, a concavidade da função é voltada para baixo e, se for positiva, a concavidade é voltada para cima.
Como a derivada segunda aponta o crescimento e decrescimento da derivada primeira, então quando a derivada segunda for negativa, a derivada primeira será decrescente e caso seja positiva, a derivada primeira será crescente.
Então bora ver o gráfico aqui:
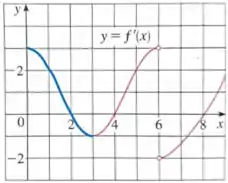
Dessa forma, analisando o gráfico, podemos ver que tem concavidade voltada para cima nos intervalos e (em vermelho) e concavidade voltada para baixo no intervalo (em azul).
Entendeu direitinho? Responde aee ;)
Resposta
Concavidade para cima em e
Concavidade para baixo em