UERJ, Sem Campus, Cálculo I, Listas de Cálculo 1 - UERJ - Lista 8, Questão 8a
O gráfico da função derivada de uma função contínua é dado abaixo
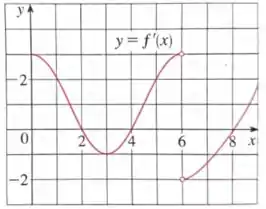
- Em que intervalos está crescendo? E decrescendo?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um gráfico de uma função derivada de uma função contínua :
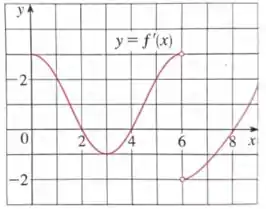
Queremos saber em que intervalos está crescendo e decrescendo?
Para isso, temos que observar os valores de para os quais é negativo!!
Se tiver pensando: “Eu, mas não teria que ver se a reta em determinado ponto estaria crescendo ou decrescendo?”
Nesse caso o gráfico teria que ser . No nosso caso já estamos vendo o gráfico da derivada😉.
Eaí? Bora lá resolver?
😉
Passo 2
Então... se observarmos o gráfico, teremos que os únicos valores negativos de são esses destacados:
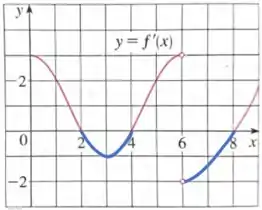
Dessa forma, temos que a é crescente nos intervalos , e . E decrescente em e .
Entendeu direitinho? Responde aee ;)
Resposta
é crescente nos intervalos , e . E decrescente em e .