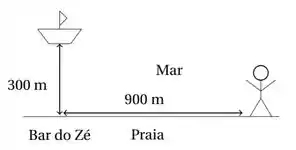
Um triatleta se encontra numa praia reta, a 900 m do Bar do Zé, quando vê uma criança cair de um barco no mar a 300 m da praia, na altura deste bar, como ilustrado abaixo. Se o atleta corre na areia a 500 m/min e nada a 400 m/min, determine o caminho que ele deve escolher para chegar o mais rápido possível ao resgate da criança. Quanto tempo vai demorar para percorrer este caminho? (Obs:300² + 400² = 500²).
Passo 1
O atleta corre uma distância x na praia e depois uma distância y no mar, diretamente na direção da criança. Portanto, o tempo em minutos do percurso é .
A distância y nadada é dada por , onde z é a distância do bar até o ponto a partir da qual o atleta começa a nadar, e . Assim, a função a ser minimizada é
Passo 2
Estamos à procura do mínimo absoluto desta função do intervalo de . Os pontos críticos desta função se encontram onde a derivada
Se iguala a zero.
Elevando tudo ao quadrado
Fazendo raiz dos 2 lados
Outra opção é
Mas essa não faz sentido porque é maior que a distância até o bar.
Passo 3
Pelo método do intervalo fechado, basta avaliarmos t no ponto crítico e nos extremos do intervalo, o menor desses valores será o mínimo absoluto.
O menor valor é . O atleta deve correr ao longo da praia pelos primeiros 500 m e depois nadar diretamente na direção da criança. Ele vai demorar = 2.25 min para chegar lá
Resposta
O atleta deve correr ao longo da praia pelos primeiros 500 m e depois nadar diretamente na direção da criança. Ele vai demorar = 2.25 min para chegar lá