Um anel condutor de raio está no plano e centrado na origem de um sistema de coordenadas. Outro anel condutor , concêntrico a possui raio , conforme a figura.
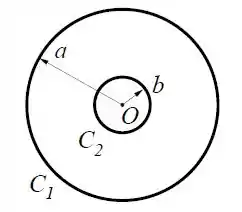
Calcule a indutância mútua entra os dois anéis. Justifique as aproximações feitas.
No anel circula uma corrente . Calcule a força eletromotriz induzida no anel 1 pelo anel 2.
Dado: O campo magnético no centro de um anel de raio por onde passa uma corrente é .
Passo 1
Calcule a indutância mútua entra os dois anéis. Justifique as aproximações feitas.
Por definição, a indutância mútua é dada por:
Como , é razoável dizer que o campo magnético no interior de , gerado pela corrente que passa por corresponderá ao campo magnético no centro do anel e será, aproximadamente:
Que corresponde ao campo magnético no centro do anel.
O fluxo magnético no anel , então, será dado por:
Agora ficou fácil calcular a indutância mútua:
Como se trata apenas de um anel, . Simplificando a expressão acima:
Passo 2
No anel circula uma corrente . Calcule a força eletromotriz induzida no anel 1 pelo anel 2.
Se o cara falou de fem induzida, temos que pensar logo em Lei de Faraday, que é dada por:
Esse é um meio de resolver o problema. Um outra forma de resolver é utilizando a definição de indutância mútua na Lei de Faraday:
Como trata-se apenas de um anel e a Lei de Faraday pode ser reescrita como:
Esse meio de resolver, nesse caso, vai facilitar a nossa vida porque nós já calculamos a indutância mútua . Então vamos seguir com ela.
Resposta