Dois fios longos e paralelos, cada um de raio , cujos centros estão separados por uma distância , são percorridos por corrente iguais , mas de sentidos opostos, conforme a figura.
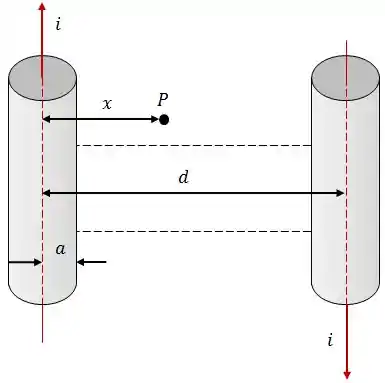
Calcule:
- O módulo, a direção e o sentido do campo magnético , no ponto , devido aos fios.
- O fluxo magnético através de um retângulo formado pelas linhas tracejadas e os dois lados externos dos fios. Considere um comprimento e despreze o fluxo dentro dos fios.
- A indutância para este par de fios.
Passo 1
- O módulo, a direção e o sentido do campo magnético , no ponto , devido aos fios.
O campo magnético gerado por um fio pode ser calculado facilmente através da lei de Ampère:
Nesse caso, a nossa curva é uma circunferência que de raio , que é a distância entre o fio e o ponto que queremos calcular o campo magnético.
Assim, o campo magnético é, resumindo a fórmula, igual a:
Vamos calcular o campo magnético de cada fio, separadamente.
- Fio da esquerda:
- Fio da direita:
Para este fio, a corrente interna será e ele se encontra a uma distância do ponto , logo:
Através da regra da mão direita, vemos que o campo magnético gerado por esse fio vai estar entrando na página.
Nesse fio passa a mesma corrente , mas ele está a uma distância do ponto . Portanto:
Novamente, pela regra da mão direita, o campo magnético gerado por esse fio estará entrando na página.
Como acabamos de ver, os dois fios geram campos magnéticos que “entram na página” no ponto . Portanto, o campo magnético resultante será:
Onde apontando para dentro da página.
Passo 2
Por definição, o fluxo magnético é dado por:
Podemos dizer que e, substituindo a expressão do campo magnético que encontramos no passo 1, teremos:
Como o problema nos disse para desprezar o fluxo dentro dos fios, vai variar entre e . Continuando...
Passo 3
Por definição, a indutância é dada por:
Esse par de fios funciona como uma espira única. Portanto, .
Resposta
a.
Apontando para dentro do plano da página.
b.
c.