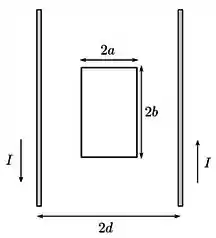
Uma espira condutora retangular de lados e é posicionada no mesmo plano que um par de fios condutores finos, retilíneos, infinitos e paralelos, como mostrado na figura abaixo. Os fios transportam correntes estacionárias de mesma intensidade e sentidos opostos e estão separados por uma distância , como indicado. O centro da espira está equidistante dos fios e os lados de comprimento são paralelos a eles. Determine a indutância mútua entre a espira e o par de fios.
Passo 1
Sabemos que cada fio produz um campo magnético com módulo dado por:
onde é a distância entre um fio e o ponto considerado. Utilizando a regra da mão direita, vemos que ambos os fios produzem campos que apontam no mesmo sentido ao longo da espira: para fora do plano do papel.
Como o centro da espira está equidistante dos fios, dois de seus lados são paralelos a eles e a corrente que atravessa cada fio tem a mesma intensidade, por simetria, o fluxo de campo magnético produzido por cada fio através da espira deve ser o mesmo. Assim sendo, o fluxo total é o dobro do fluxo produzido por um fio.
Passo 2
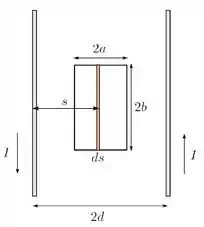
Vamos considerar o fio à esquerda da espira. Consideramos uma tira de área infinitesimal de comprimento e largura , como mostrado na figura abaixo. Esse elemento está a uma distância do fio. O fluxo produzido pelo fio através da tirinha será:
Aqui, escolhemos o vetor normal ao plano da espira no mesmo sentido de .
O fluxo através da espira (considerando apenas o fio da esquerda!) será:
Considerando, agora, os dois fios, o fluxo total de campo magnético através da espira será:
Passo 3
Por fim, utilizamos a definição de indutância mútua para obter a indutância mútua entre o par de fios e a espira: