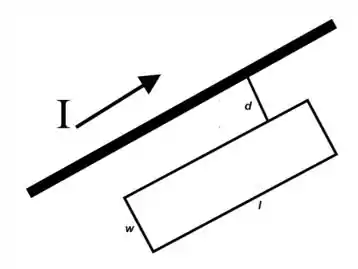
Uma espira retangular está no mesmo plano de um fio longo retilíneo que conduz uma corrente . A espira tem um comprimento (paralelo ao fio) e largura , conforme figura. A indutância mútua do sistema dobrará em qual (is) dos seguintes casos?
- Dobrando-se .
- Dobrando-se
- Dobrando-se .
- Reduzindo-se pela metade.
- II e III;
- I, III e IV;
- I, II, III e IV;
- Somente I;
- Somente III.
Passo 1
POW! De acordo com a teoria, o fluxo de campo magnético que o fio longo faz dentro da espira pode ser dado por...
Onde é indutância mútua que tanto queremos encontrar!
Passo 2
Então, a nossa primeira tarefa é determinar o fluxo do campo dentro desse retângulo que ele deu aí.
E pode anotar aí: toda vez que um problema te pedir fluxo é porque ele na real quer que você resolva uma integral de superfície:
Onde é a região retangular onde ele quer o fluxo do campo .
Acho que você vai concordar comigo que dentro desse retângulo o campo magnético é sempre pra dentro devido à regra da mão direita...
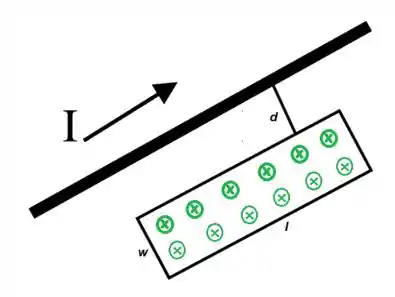
A diferença é que os pontos mais próximos do fio terão um campo mais intenso (por isso as bolinhas estão mais escuras).
Bem, mas de uma coisa é certo, o representa o vetor normal unitário da superfície é sempre na mesma direção que o campo magnético. Ou seja, na direção saindo da sua tela. Então...
Como é um versor (vetor unitário)...
Seria muito bom a gente tirar o campo magnético de dentro da integral, neh? Mas porque a gente não pode fazer isso?
ORA! Porque o campo muda de intensidade dentro da superfície retangular . Saca? E ele muda a intensidade com a distância . O valor do campo magnético para fio longo é...
Para resolver essa integral aí, precisamos encontrar uma relação de com .
Passo 3
Vamos considerar a região como a soma de váaarios retângulosinhos de largura e comprimento ...
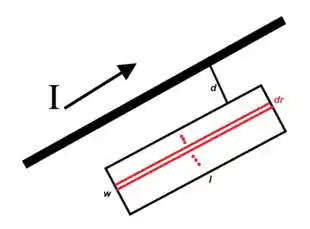
Assim, pomos falar que a unidadezinha de área é...
E para formar a região toda, a gente soma os retangulinhos começando de a vai até . Portanto...
Por propriedade de Log...
Passo 4
Então, como comentamos no passo ...
PRONTINHO! Essa daí é a indutância mútua!
Repare que se dobrar o tamanho de , a indutância mútua dobra também, mas devido ao dobrar ou reduzir pela metade não é o suficiente para dobrar , saca? Então a única alternativa correta é a letra E.
Resposta
Letra E.