Uma espira quadrada condutora de lado e resistência está orientada paralelamente a um fio condutor infinito a uma distância .
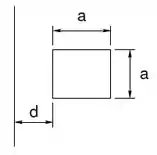
(a) Calcule a indutância mútua do sistema.
(b) Se o fio infinito é percorrido de baixo para cima por uma corrente , onde é o tempo e é uma constante positiva, calcule a corrente induzida na espira quadrada. Determine e explique o sentido da corrente induzida.
Passo 1
O campo magnético que o fio produz quando é percorrido por uma corrente (de baixo para cima) é dado por:
onde é a distância ao ponto onde se está calculando . Pela regra da mão direita, aponta para dentro do plano da espira.
Considerando que o vetor normal também aponta para dentro do plano, o fluxo na espira pode ser calculado como:
Assim sendo, indutância mútua será dada por:
Passo 2
A fem induzida na espira é dada por:
Como ,
Logo, a corrente induzida em módulo será:
O sentido pode ser obtido a partir da lei de Lenz:
- A corrente está aumentando, logo o campo magnético aumenta e, consequentemente, o fluxo magnético também aumenta;
- Se o fluxo aumenta, a corrente induzida precisa se opor a esse aumento;
- Isso significa que a corrente induzida terá sentido anti-horário.
Resposta
(a)
(b) , no sentido anti-horário.