Parte :
Considere um solenóide ideal de espiras, raio e comprimento transportando uma corrente no sentido indicado pela figura abaixo. O campo magnético em seu interior é dado por .
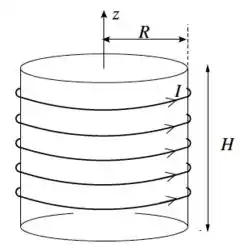
- Determine a auto-indutância do solenóide.
- Considere, agora, que a corrente elétrica seja variável no tempo , sendo uma constante. Determine o vetor campo elétrico induzido nas regiões (dentro do solenóide) e (fora do solenóide).
Passo 1
a) Antes de começar, precisamos nos lembrar que a definição de auto-indutância é
ou seja, é definida como o fluxo por unidade de corrente indutora.
Bom, uma vez que recordamos disso, precisamos calcular o fluxo do campo magnético através das espiras do solenóide. O campo magnético, como é dado no enunciado, tem a direção e sentido do eixo positivo e tem o mesmo valor em todos os pontos dentro do solenóide, por isso, é uniforme dentro do solenóide. Fora do solenóide (ideal!), .
Para calcular o fluxo, precisamos também definir um vetor área orientado. Vamos escolher esse vetor paralelo ao vetor , como desenhamos na figura abaixo.
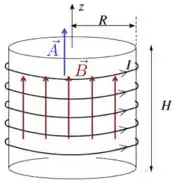
Bom, colocando isso dentro da expressão para o fluxo magnético, que é vezes o fluxo através de uma única espira , teremos
Portanto, a auto-indutância tem valor
Repara, nessa expressão, que a auto-indutância não depende da corrente que passa nas espiras e é diretamente proporcional e à área de de cada espira.
Passo 2
b) Como a corrente agora depende do tempo, o campo magnético que ela produz dentro do solenóide também dependerá do tempo. Isso significa, de acordo com o grande Maxwell, que haverá um campo elétrico induzido em . Da mesma maneira do que no caso anterior, o campo fora para é nulo.
Portanto, para este item, vamos precisar da lei de Faraday escrita da seguinte maneira:
Para
Vamos considerar como nossa curva fechada um círculo de raio , como na figura abaixo.
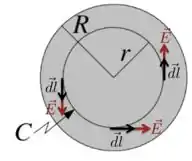
Como estamos considerando um solenóide ideal, ou seja, um solenóide com , então temos um solenóide bastante longo na direção do eixo . Nesse caso, se a gente pegar esse solenóide e girá-lo em torno do eixo , o solenóide continua o mesmo, o que acontece também quando o transladamos ao longo desse mesmo eixo . Ou seja, temos um problema que tem simetria cilíndrica.
Isso significa que o campo elétrico tem o mesmo valor em todos os pontos da curva fechada , portanto, só pode depender de , não tendo nenhuma componente ao longo de e nem componente ao longo da direção radial.
Passo 3
b) Continuação...
Para
Por isso, como mostrado na figura acima, o vetor campo elétrico deve ser:
Tendo com essas características, vamos tomar o elemento da curva fechada como , ou seja, na mesma direção e sentido de . Colocando isso no lado esquerdo da lei de Faraday, teremos
Agora, vamos olhar para o lado direito dessa lei, em que a gente tem o fluxo do campo magnético. Como o campo é uniforme dentro do solenóide (ideal!!) e também dependo do tempo, o fluxo é:
em que é a área do círculo fechado da figura. É IMPORTANTE ficarmos ligados aqui, porque na expressão para o fluxo magnético da expressão anterior, só precisamos tomar o fluxo através da área , sem precisar multiplicar por , como fizemos para calcular o fluxo total do solenóide todo do item a. FICA LIGADO NISSO, OK?
Sabendo que o campo magnético neste caso é dado por
temos, já igualando os dois lados da lei de Faraday
que dá um vetor campo elétrico
No próximo passo, veremos como fica o campo elétrico para .
Passo 4
b) Continuação...
Para :
Para esse caso, ainda continuam valendo as características do campo elétrico que tiramos da simetria cilíndrica do problema, ou seja, . Portanto, podemos também usar . Então, o lado esquerdo da lei de Faraday continua sendo: . Vamos ver agora como fica o lado direito, que tem a taxa temporal de variação do fluxo magnético.
Para essa região, como mostra a figura abaixo, como o campo magnético é zero para , o fluxo magnético do campo total será através da área .
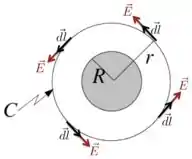
Com isso,
Simplificando, é
Repara que, embora não haja campo magnético para , existe campo elétrico porque o campo magnético em está variando com o tempo! ISSO É MUITO IMPORTANTE...
Resposta
a)
b)