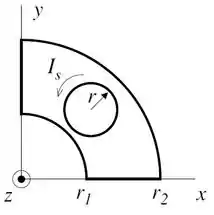
Um circuito com resistência , contido no plano , é constituído por dois arcos de circunferência com raios e e por dois segmentos retos. Este circuito envolve um solenoide muito longo, com eixo paralelo ao eixo , espiras por unidade de comprimento e raio tal que , conforme a figura. Pelo solenoide passa uma corrente que flui no sentido anti-horário. cresce com o tempo com taxa . Desprezando efeitos de borda, a intensidade do campo magnético no interior do solenoide é .

(a) (1,0 ponto) Calcule o fluxo do campo do solenoide através do circuito.

(b) (1,0 ponto) Calcule o coeficiente de mútua indutância entre o solenoide e o circuito.

(c) (1,0 ponto) Calcule o sentido (horário ou anti-horário) e a magnitude da corrente induzida no circuito.

Assim sendo,

O coeficiente de mútua indutância entre o solenoide e o circuito, por definição, é dado por:

Vamos inicialmente determinar o sentido da corrente. Ele pode ser determinado pela lei de Lenz. Pensa comigo:

1. Como o campo dentro do solenoide aumenta com o tempo, o fluxo magnético através do circuito também aumenta, certo?
2. Assim sendo, a corrente induzida no circuito deve gerar um campo magnético que irá se opor a este aumento.
3. Logo, a corrente induzida tem sentido horário.

Sacou? A ideia é sempre pensar que o sistema busca um equilíbrio!

Agora, utilizamos a lei de Faraday para encontrar a fem induzida.

já que .

A corrente induzida será dada, portanto, por:

onde é a resistência do circuito.

Reparem que a corrente induzida é negativa! Isso porque, no começo da questão, escolhemos o sentido anti-horário como o positivo. Ou seja, possui sentido horário, concordando com a nossa análise pela lei de Lenz.