Uma espira condutora quadrada de lado e a resistência está orientada paralelamente a um fio condutor infinito percorrido por uma corrente , a uma distância .
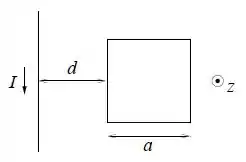
- Calcule a indutância mútua do sistema. Escolha a normal à espira no sentido positivo do eixo . Obs: o campo magnético a uma distância de um fio infinito percorrido por uma corrente é .
- Para com , calcule a corrente induzida na espira quadrada e determinar seu sentido. (justifique a sua resposta)
Passo 1
- Calcule a indutância mútua do sistema. Escolha a normal à espira no sentido positivo do eixo . Obs: o campo magnético a uma distância de um fio infinito percorrido por uma corrente é .
- Para com , calcule a corrente induzida na espira quadrada e determinar seu sentido. (justifique a sua resposta)
A definição de indutância mútua é:
Como se trata de apenas uma espira, :
A parada agora é calcular o fluxo do campo magnética.
Passo 2
Onde e . Logo:
Voltando para a fórmula da auto-indutância:
Passo 3
Vamos achar primeiro o valor da corrente. De acordo com a Lei de Faraday:
Onde:
Logo:
Uma vez que encontramos a fem induzida, fica tranquilo de calcular a corrente induzida:
Passo 2
Pra achar o sentido, primeiro a gente tem que saber pra onde aponta o campo magnético gerado pelo fio. Usando a regra da mão direita, com o polegar apontando pro sentido da corrente , a gente conclui que o campo magnético que atravessa a espira aponta no sentido positivo de . E como a corrente aumenta com o tempo, esse campo também vai aumentar com o tempo, certo? Até aqui tranquilo?
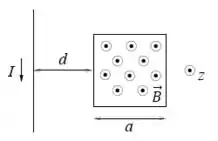
Agora, pela Lei de Lenz:
O sentido de qualquer efeito de indução magnética é tal que ele se opõe à causa que produz esse efeito.
Pra que a indução magnética na espira se oponha à do fio, a corrente induzida tem que gerar um campo entrando no papel, no sentido negativo de . Pela regra da mão direita, se o campo induzido entra no papel, a corrente tem que estar no sentido horário!