Um capacitor de fica completamente carregado quando conectado a uma bateria de . Depois disso, desliga-se a bateria e liga-se o capacitor carregado a um indutor de . A máxima corrente que passa pelo indutor é aproximadamente:
- ;
- ;
- ;
- ;
- ;
Passo 1
Pow! Antes de tudo, vamos desenhar esse circuito aí beleza?
Bem, após o capacitor ficar completamente carregado (com a mesma tensão que a fonte), ele se conecta com um indutor:
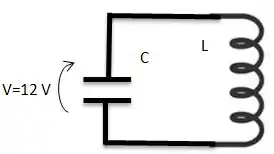
E imediatamente após ele se conectar ao indutor de indutância , surge uma corrente para carregar o indutor:
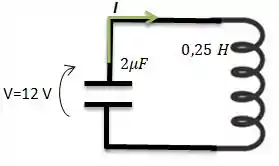
E é justamente essa corrente que queremos obter!
Passo 2
Pode anotar uma coisa aí: toda vez que você tiver um circuito (formado por um indutor e um capacitor apenas) a energia no sistema se conserva. Estou te falando isso, porque uma das formas mais fáceis de determinar a máxima corrente que circula no circuito é por conservação de energia:
Ou seja, a energia do capacitor é igual a armazenada no indutor! De acordo com a teoria...
Olha a nossa amiga corrente aparecendo aí!
Então...
Logo, substituindo esses dados dado no problema (lembre-se de que )...
Portanto, a máxima corrente será...
Resposta
Letra C.