Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Indutores e Indutância

Ver Teoria
Exercício 3512345678910111213141516171819202122232425262728293031323334363738394041424344454647484950515253

Enunciado

UFPE- Sem Campus - Física 3-Provas Antigas -1 EE - 2021.2 – Questão 1

R e raio externo 3 R / 2 que é completamente preenchido por um material não condutor (dielétrico) de constante dielétrica k . A diferença de potencial entre as paredes condutoras interna ( r   =   R ) e externa ( r   =   3 R / 2 ) do capacitor é V . Nas regiões 0 ≤ r < R e r > 3 R / 2 existe vácuo, cuja permissividade elétrica é denotada por ε 0 . Nessas circunstâncias:

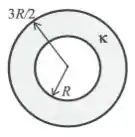
  1. Deduza a expressão da capacitância C deste capacitor. Expresse seu resultado em termos de k , R e ε 0 . Atenção: não use expressão “memorizada” para C .
  2. Calcule a carga elétrica livre Q sobre a parede condutora interna de raio R . Expresse seu resultado em termos de k , R , ε 0 e V .
  3. Calcule a carga elétrica induzida Q ' na substância não condutora, nas proximidades da parede interna de raio R . Expresse seu resultado em termos de k , R , ε 0 e V .

Passo 1

Fala galerinha, tudo tranquilo??? Vamos lá resolver essa questão

Aqui no item a), precisamos deduzir uma expressão pra capacitância. Você lembra como deduzimos? Então relaxa e vem comigo que eu te mostro! Precisamos primeiro ter em mente que a capacitância com dielétrico é dada por:

C = k C 0 , onde C 0 é a capacitância sem dielétrico e k é a constante dielétrica.

Como temos que escrever essa fórmula em função de k , R e ε 0 , podemos considerar a capacitância como:

C 0 = Q / V , onde V =   ∫ E → d S → .

Após descobrirmos o potencial e substituirmos em C 0 , trocaremos o C 0 da outra equação pela equação encontrada. Parece meio confuso, mas você vai entender (✿◠‿◠)

Passo 2

Primeiro acharemos o potencial!!

V =   ∫ E → d S →

Mas quem é o campo elétrico? Através da lei de Gauss, temos:

∮ E → d A → = q i n t ε 0

O campo é constante e como está na mesma direção e d A → , precisamos descobrir ∮ d A → apenas e substituir na fórmula.

Em coordenadas esféricas:

d A → =   r 2 sin ⁡ θ d θ d ∅ â r

Logo, aplicando a integral:

∮ d A → = ∫ 0 2 π ∫ 0 π r 2 sin ⁡ θ d θ d ∅ â r

Desenvolvendo:

∮ d A → = r 2 ∫ 0 2 π d ∅ ∫ 0 π sin ⁡ θ d θ â r

∮ d A → = r 2 2 π . - 1 . c o s ⁡ ( θ ) π 0 â r

∮ d A → = r 2 2 π . 2 â r

∮ d A → = 4 π r 2 â r

Substituindo, temos

E 4 π r 2 = Q ε 0

E = Q 4 π r 2 ε 0

Agora que temos o campo, podemos substituir na fórmula do potencial.

V = ∫ R 3 R / 2 Q 4 π r 2 ε 0 d r

V = Q 4 π ε 0 ∫ R 3 R / 2 1 r 2 d r

V = - 1 Q 4 π ε 0 . 1 r 3 R / 2 R

V = Q 4 π ε 0 1 R - 2 3 R

V = Q 4 π ε 0 1 R - 2 3 R

V = Q 4 π ε 0 3 - 2 3 R

V = Q 12 π ε 0 R

Substituindo em C 0 = Q V , temos:

C 0 = Q Q 12 π ε 0 R

C 0 = 12 π ε 0 R

Finalmente podemos encontrar a capacitância

C = k C 0

C = 12 π ε 0 k R

Passo 3

B)

Sabendo que a capacitância é dada por C = Q V , ao isolarmos a carga Q e colocarmos C em função de k , R , ε 0 e V , temos:

C = Q V

Q = C V

Q = 12 π ε 0 k R V

Passo 4

Para descobrirmos a carga pedida temos que levar em consideração que o campo elétrico com dielétrico é igual a:

E = E 0 - E ´             ( I )

Onde E 0 é o campo sem dielétrico produzido pelas cargas livres nas placas condutoras do capacitor. A partir disso, vamos desenvolver essa fórmula e isolarmos Q´ para descobrirmos a resposta.

Como o dielétrico preenche todo o espaço entre as placas condutoras, sabemos que E = E 0 / k .

Substituindo em ( I ) , temos

E = E 0 - E ´  

E 0 k = E 0 - E ´  

E ´   = E 0 - E 0 k

E ´   = E 0 1 - 1 k

E ´   = E 0 k - 1 k             ( I I )

Sabe-se que o deslocamento elétrico é dado por:

D = ε 0 E

Logo,

E ´ = D ´ ε 0       e         E 0 = D ε 0

Como o deslocamento é a carga dividida pela área, podemos reescrever as fórmulas anteriores assim:

E ´ = Q ´ ε 0 A       e         E 0 = Q ε 0 A

Agora substituindo em ( I I ) temos:

Q ´ ε 0 A   = Q ε 0 A k - 1 k

Q ´   = Q k - 1 k

Substituindo a carga Q pela fórmula obtida na letra b), temos:

Q ´ = 12 π ε 0 k R V k - 1 k

Q ´ = 12 π ε 0 ( k - 1 ) R V

E assim encerramos essa questão! O que acharam da resolução? Deixe seu feedback

Um abraço e até a próxima!! (/◕ヮ◕)/

Bons Estudos! :)

Resposta

  1. C = 12 π ε 0 k R

  2. Q = 12 π ε 0 k R V

  3. Q ´ = 12 π ε 0 ( k - 1 ) R V

Exercícios de Livros Relacionados

Dois solenoides tem o mesmo comprimento e raio, e os núcleos de ambos contêm cilindros idênticos de ferro. Entretanto, o solenoide A tem três vezes o número de voltas por comprimento que o solenoide B
31- Um solenoide fino possui 400 espiras por metro e raio igual a 1.10c m . A corrente no solenoide cresce com uma taxa uniforme d i / d t . O campo elétrico induzido em um ponto próximo do centro do
29- O campo magnético no interior de um solenoide retilíneo longo, com seção reta circular de raio R , está crescendo com uma taxa d B / d t . ( a ) Qual é a taxa de variação do fluxo magnético atravé
32- Um anel metálico de 4.50c m é colocado entre os pólos norte e sul de grandes ímãs, cujos planos da área são perpendiculares ao campo magnético. Esses ímãs produzem um campo inicial uniforme de 1.1
33- Um solenoide longo, com seção reta de área igual 8.0c m 2 , contém 90e s p i r a s por metro e conduz uma corrente igual a 0.350A . Um segundo enrolamento com 12 espiras circunda o centro do solen