- Calcule o vetor campo magnético produzido por um longo fio condutor, de diâmetro desprezível, que repousa no eixo dos de um sistema de coordenadas cartesianas, e que transporta uma corrente sentido positivo do eixo dos .
- Uma corrente circula em uma espira formada por dois segmentos radiais e duas semicircunferências de raios e com um centro comum no ponto (veja figura abaixo). Calcule o módulo e o sentido (para dentro ou para fora da página) do vetor campo magnético no ponto .
- Calcule o módulo e o sentido do vetor momento magnético da espira
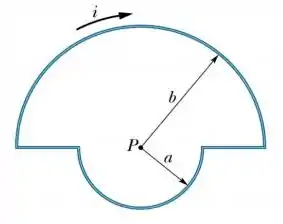
Passo 1
Cara... Essa letra A não tem muito haver com a espira. Essa espira é mais para a letra B e letra C, ta legal?
Na letra A, queremos apenas calcular o módulo do campo magnético em todos os pontos do espaço feitos por uma corrente sendo transportada por um fio longo repousando sobre o eixo ...
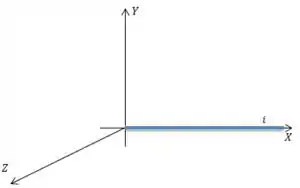
Vamos usar para isso a Lei de Ampére, beleza?
Passo 2
Podemos e vamos usar aqui a Lei de Ampère, já que de acordo com ele...
A Amperiana vai ser um circulo de raio ao redor desse fio...
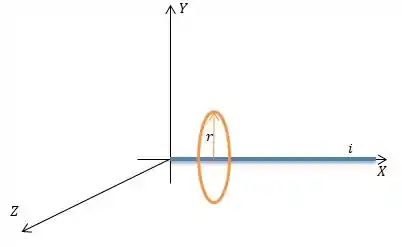
Pow, o campo magnético gerado por esse fio é sempre paralelo ao vetor tangente ...
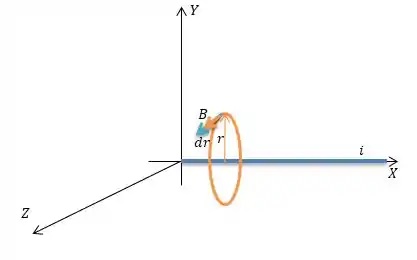
De modo que , então, pela Lei de Ampère...
O campo em cima dessa circunferência de raio é sempre constante, de modo que podemos tira-lo da integral...
A integral de é o comprimento da curva. Como no nosso caso é uma circunferência de raio ...
Como é era de se esperar neh. Já que o fio é longo (indo para o infinito).
Passo 3
Agora vai começar outra parte do exercício no qual a gente vai determinar o valor do campo elétrico no ponto feito por essa espira...
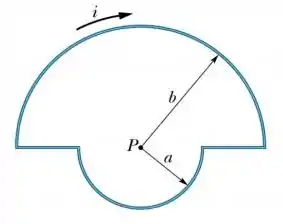
Bem, como o ponto está em cima da continuação dos segmentos retos, estes não vão interferir no campo magnético. Então, o módulo do campo magnético produzido nesse ponto , vai ser a soma dos módulos produzidos por cada uma dessas semicircunferências...
Onde é o campo magnético produzido pela parte de cima da semicircunferência.
Cara, podemos resolver esse problema usando a Lei de Biot-Savart! Vamos nessa?
Passo 4
De acordo com Biot-Savart, podemos encontrar o campo elétrico através da fórmula...
Onde é o vetor de direção da corrente e é o vetor de distância da corrente ao ponto onde se está medindo o campo elétrico (centro)...
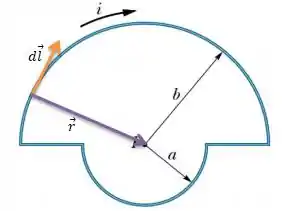
Ora... O módulo do produto vetorial é...
Onde é o ângulo entre o vetor e que é . Só que pela regra ad mão direita, o sentido do produto vetorial é para dentro ()...
Então...
Ou seja, pela regra de Briot-Savart...
Só que quem é a integral de ???
Passo 5
Ora... A integral de é o comprimento da curva de cima. No caso, a curva é uma semicircunferência de raio . Então o seu comprimento será...
Então...
Passo 6
E olha que massa... Para a circunferência de baixo, o campo magnético vai ser o mesmo, porém...
Então, o campo magnético total no ponto ...
Onde o menos significa que o campo é para baixo (ou para dentro da sua telinha).
Passo 7
O vetor momento magnético da espira tem módulo...
Onde é a área da espira. O sentido do momento é então dado pela regra da mão direita, ou seja, também tem sentido entrando na sua telinha ()...
Passo 8
Então basta calcular a área da espira...
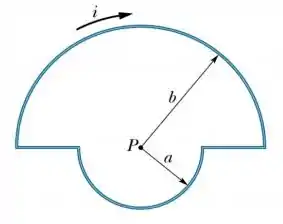
Ora...
Então, o vetor momento magnético será...
Resposta
Letra A:
Letra B:
Letra C: