6 - Encontre a aceleração resultante instantânea de uma partícula se movendo em um círculo de raio , se a velocidade angular instantânea for de e a aceleração tangencial for de . Expresse o ângulo do vetor aceleração resultante em relação ao vetor de velocidade tangencial.
- a
- a
- a
- a
- a
Passo 1
Ora, neste problema é interessante a gente desenhar essa partícula se movendo neste circulo e colocar as acelerações que ela vai ter:
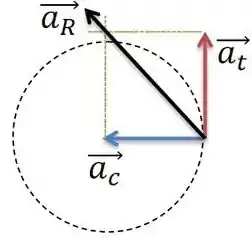
A aceleração tangencial é a aceleração de . A aceleração é a aceleração centrípeta, enquanto que a é a aceleração total (que é quem queremos encontrar ).
Ora! Como temos a aceleração tangencial, se encontrarmos a aceleração centrípeta, o nosso problema vai estar resolvido, já que a aceleração total é Pitágoras das duas! Então, partiu encontrar a aceleração centrípeta!
Passo 2
Ora, podemos encontrar a aceleração centrípeta a partir da velocidade angular dessa maneira aqui:
No nosso caso, essa velocidade angular foi dada, mas ela foi dada em (rotações por minuto):
Como estamos trabalhando no sistema internacional, a dimensão do SI para é . Podemos passar para lembrando que uma rotação é e minuto é , ou seja...
Então, basta multiplicar por ...
Logo, a aceleração centrípeta será...
Passo 3
A aceleração total, então será dada por Pitágoras entre a aceleração tangencial e a aceleração centrípeta:
Já sabemos então que a letra A é a correta, mas pra você que está curioso e quer saber como se encontra o ângulo que ele pediu, venha comigo!
Passo 4
O ângulo pedido foi o ângulo entre a tangencial e a aceleração total:
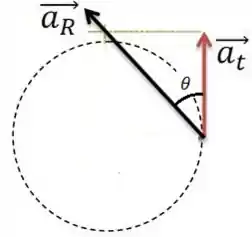
Esse ângulo , faz com que a aceleração tangencial se relacione com a total pela trigonometria dessa forma aqui:
Logo...
Substituindo então e isolando...
O arco cujo cosseno vale é...
Saca?
Resposta
Letra A.