Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Circular Acelerado

Ver Teoria
Exercício 461234567891011121314151617181920212223242526272829303132333435363738394041424344454748495051525354555657

Enunciado

USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 41a

41. Uma bola homogênea de raio r rola sem deslizar, a partir do repouso, desde o topo de um domo hemisférico de raio R .

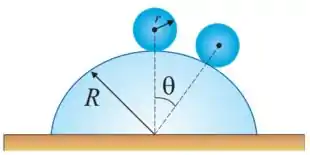
(a) Depois de percorrer que ângulo θ em relação à vertical a bola deixará a superfície?

Passo 1

Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉

Nesse problema temos uma bola de raio r localizada no topo de uma semiesfera de raio R . A bola rola em direção ao solo sem deslizar.

Com isso, queremos saber qual ângulo θ com a vertical a bola deixa a superfície.

Tem ideia de como fazer isso? 😬

O que vai acontecer é que a bola começa a acelerar e em um ponto a bola deixará de ter contato com a semiesfera.

A força centrípeta no ponto onde a bola se descola com a superfície é dada por

F c = m v 2 R

Nesse ponto também a força peso é dada por

F p = m g c o s θ

A partir daí, vamos aplicar a lei da conservação de energia para obter a velocidade v e manipular nossas equações para determinar θ de alguma forma.

Parece difícil? 😐

Passo 2

Podemos afirmar que F c = F p , ou seja

m v 2 R = m g c o s θ

v 2 R = g c o s θ

v 2 = R g cos ⁡ θ

Pela lei da conservação de energia, podemos afirmar que a energia inicial do sistema é igual a energia final, ou seja

Inicialmente a energia no sistema é composta unicamente pela energia potencial gravitacional da bola

E i = m g R

Já no instante final, a bola possui energia potencial, energia de translação e energia de rotação

E f = I ω 2 2 + m v 2 2 + m g R cos ⁡ θ

Igualando E i com E f ...

m g R = I ω 2 2 + m v 2 2 + m g R cos ⁡ θ

O momento de inercia de uma bola é dada por I = 2 m R 2 5 e podemos relacionar ω com v a partir da equação ω = v R ...

m g R = 2 m R 2 5 v R 2 2 + m v 2 2 + m g R cos ⁡ θ

m g R = 2 m R 2 v 2 10 R 2 + m v 2 2 + m g R cos ⁡ θ

Simplificando e isolando v

g R = 2 v 2 10 + v 2 2 + g R cos ⁡ θ

g R = 2 10 + 1 2 v 2 + g R cos ⁡ θ

2 10 + 1 2 v 2 = g R - g R cos ⁡ θ

7 10 v 2 = g R 1 - cos ⁡ θ

v 2 = 10 g R 1 - cos ⁡ θ 7

Tranquilo até aqui? 😎

Passo 3

Igualando v 2 das duas equações que obtemos, vamos encontrar

R g cos ⁡ θ = 10 g R 1 - cos ⁡ θ 7

7 R g cos ⁡ θ = 10 g R - 10 g R cos ⁡ θ

Isolando cos ⁡ θ ...

7 R g cos ⁡ θ + 10 g R cos ⁡ θ = 10 g R

7 R g + 10 R g cos ⁡ θ = 10 g R

1 7 R g cos ⁡ θ = 10 g R

cos ⁡ θ = 10 17

Calculando o arco cosseno de 10 17 ...

θ = cos - 1 ⁡ 10 17

θ = 54 °

Sacou como faz? Responde Aí! 😉

Resposta

θ = 54 °

Exercícios de Livros Relacionados

O volante de uma máquina a vapor gira com uma velocidade angular constante de 150r e v / m i n . Quando a máquina é desligada, o atrito dos mancais e a resistência do ar param a roda em2,2h . (a) Qual
O prato de um toca-discos está girando a 33 1 3r e v / m i n . Uma semente de melancia está sobre o prato a 6,0c m de distância do eixo de rotação. (a) Calcule a aceleração da semente, supondo que ela
Na Figura 9.38 , o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui um
Um roda começa a girar a partir do repouso em t= 0 com aceleração angular constante. No instante t=2,0s , a velocidade angular da roda é 5,0r a d / s . A aceleração cessa abruptamente no instante t=20
Um carro parte do repouso e se move em uma pista circular com 30,0m de raio . A velocidade do carro aumenta a uma taxa constante de 0 , 500m / s 2 . (a) Qual é o módulo da aceleração linear média do c