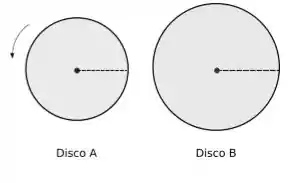
A figura mostra dois discos que podem girar em torno de seus centros independentemente. No instante , as retas de referência dos dois discos têm a mesma orientação (como mostrado no desenho); o disco já está girando com uma velocidade angular constante e o disco parte do repouso com uma aceleração angular constante de.
a) Em que instante as duas retas de referência têm o mesmo deslocamento angular ?
b) Qual será o primeiro instante , após , para o qual as duas retas de referência estão paralelas com a linha que une o centro dos dois discos?
c) Considere agora que o deslocamento angular do disco varia no tempo com , onde está em radianos. Em qual instante a velocidade angular de é igual à velocidade angular de ?
Passo 1
Fala aí! Bom, os deslocamentos angulares dos discos são:
Como elas tem o mesmo deslocamento, igualando os dois, temos:
Já foi uma parte!
Passo 2
A sacada aqui é perceber que as retas de referência estarão alinhadas quando os deslocamentos forem separadamente múltiplos de ou . Sacou?
Na real, podemos dizer que os deslocamentos serão múltiplos (distintos) de , já que serão também múltiplos de , né?
Para o disco , é necessário que:
Portanto:
Então, isso significa que:
Com isso, concluímos que, se:
Teríamos:
e
Viu que para qualquer e eles serão múltiplos de ? Portanto, a primeira vez que se encontram é quando , e então
Passo 3
Para obter a velocidade angular, é só derivar a posição!
Assim, implica em:
E então:
Resposta
a)
b)
c)