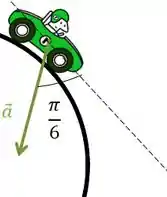
A aceleração de um corpo faz um ângulo de com a tangente do movimento, como mostrado na figura abaixo. Determine a equação que relaciona a velocidade angular e a aceleração angular.
Passo 1
Nós sabemos que a aceleração tangencial pode ser relacionada com a aceleração angular.
E a aceleração centrípeta é
Mas queremos a velocidade angular e não a escalar, lembrando que
E substituindo na equação pra aceleração centrípeta, fica
Tá mas e agora?
Passo 2
Como ele deu o ângulo podemos faz as componentes da aceleração, uma tangencial e outra apontando para o centro da curva, no caso a centrípeta.
Vamos usar a “regra COlado/SEparado”
Passo 3
Beleza, mas e agora?
Dividindo a aceleração tangencial pela centrípeta que temos no passo 1 vamos encontrar
Agora fazendo a mesma coisa só que com as equações do passo 2
Podemos igualar esses dois resultados
E pronto temos uma relação entre os dois.