[ENUNCIADO COMUM ÀS QUESTÕES 1 E 2]
Uma roda de raio está inicialmente em repouso. Partindo do instante a roda é acelerada a até atingir uma velocidade angular de num tempo . Em a aceleração cessa.
[QUESTÃO 1]
Sejam e respectivamente as acelerações tangencial e radial de um ponto na borda da roda imediatamente após . Podemos afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Temos uma roda sendo acelerada com uma certa aceleração angular :
Se pegarmos um ponto na borda dessa roda... quais acelerações esse ponto sofre?
Como é um movimento circular, existe uma aceleração centrípeta apontando para o centro (aceleração radial):
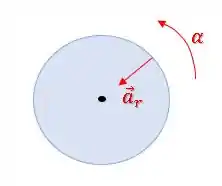
Além disso, como o movimento está acelerado por , existe uma aceleração tangencial:
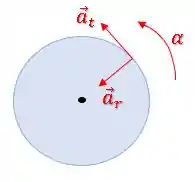
Passo 2
Mas como podemos calcular essas acelerações?
A aceleração radial pode ser calculada por:
Repara que ela depende apenas da velocidade linear ou angular (pois as duas estão relacionadas) da roda.
Assim, como a roda parte do repouso, no instante logo após , essa aceleração é nula:
Ela irá aumentar conforme a roda vai ganhando velocidade.
Passo 3
Já a aceleração tangencial pode ser calculada a partir da aceleração angular :
Assim, nem precisamos fazer contas...
Como e , temos que é maior que zero:
Então, nossa resposta fica:
Ficamos com a letra (h).
Resposta
Letra (h)