Um carretel gira em torno de seu eixo central com velocidade angular . Existe atrito com o eixo, que produz uma aceleração angular .
a) Obtenha o instante de tempo no qual o carretel para de girar.
b) No instante inicial encontre o módulo da aceleração total de um ponto na borda do carretel cuja distância ao eixo é .
Passo 1
Na letra (a), queremos saber quanto tempo o carretel leva até parar de girar.
O carretel sofre uma aceleração angular constante , logo ele realiza um movimento circular uniformemente variado.
A aceleração angular é dada por:
Passo 2
Com essa expressão, conseguimos descobrir o intervalo de tempo que durou até a velocidade angular chegar a zero.
A velocidade angular final é nula:
Substituindo os valores:
Passo 3
Na letra (b), queremos a aceleração total de um ponto na borda do carretel.
Qual é a aceleração total do bloco?
Ele tem uma componente de aceleração centrípeta, pois realiza uma trajetória circular e também apresenta uma componente de aceleração tangencial, pois o movimento circular é acelerado.
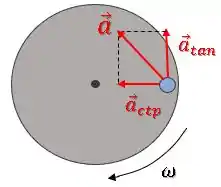
Para achar o módulo da aceleração total , usamos a seguinte relação:
Passo 4
A aceleração centrípeta será:
No instante inicial, já sabemos que a velocidade angular vale :
Enquanto a aceleração tangencial é dada pela aceleração angular vezes a distância do ponto ao eixo de rotação:
Passo 5
Assim, temos que:
Substituindo esses valores, temos:
Assim, achamos o módulo da velocidade total:
Resposta
(a)
(b)