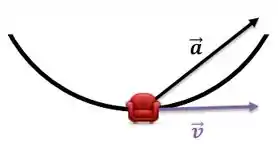
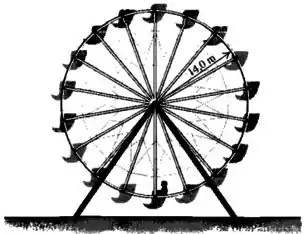
A roda-gigante da figura abaixo, gira no sentido contrário ao dos ponteiros de um relógio. Em dado instante, um passageiro na periferia da roda e passando no ponto mais baixo do movimento circular se move a e está ganhando velocidade com uma taxa de . a) Determine o módulo, a direção e o sentido da aceleração do passageiro nesse instante. b) Faça um desenho do passageiro e da roda-gigante mostrando o vetor velocidade e o vetor aceleração.
Passo 1
Pelo enunciado, considerando o movimento do passageiro, ele está em um movimento circular, e sua velocidade está aumentando.
Isso nós diz que neste caso temos aceleração centrípeta (movimento circular) e aceleração tangencial (aumento da velocidade).
Os dados do enunciado são
Passo 2
a)
Para encontrarmos a aceleração total, primeiro vamos lembrar que ela é a soma vetorial da aceleração centrípeta com a aceleração tangencial.
Precisamos então calcular primeiro a aceleração centrípeta, usando a sua fórmula
Passo 3
Vamos fazer um esquema para mostrar o valor da aceleração total,
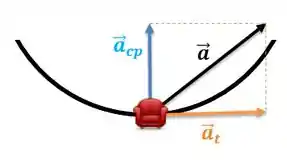
Temos cada componente
Usando a fórmula de aceleração total,
Passo 4
b)
O esquema ficará
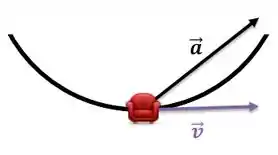
Resposta