Um corpo se desloca ao longo de uma pista curva de tal modo que o módulo de sua velocidade é maior quanto mais baixo ele se encontra, como representado na figura ().
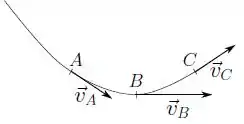
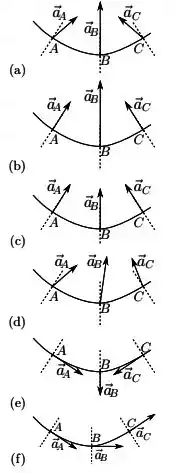
Escolha a opção que melhor representa o vetor aceleração instantânea nos pontos A, B, C.
Passo 1
Vamos lá, aqui temos que observar os dois tipos de aceleração desse movimento em curva, a Aceleração Centrípeta e a Aceleração tangencial.
A Aceleração Centrípeta é responsável por mudar a direção da velocidade, ou seja, vai existir nos três pontos, pois o carro está fazendo uma trajetória curva.
Essa componente da aceleração aponta na direção radial, ou seja, aponta para o centro do arco. A direção radial está como aqueles pontilhados em cima de cada um dos pontos:
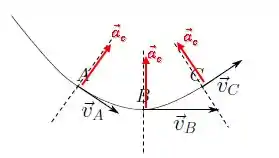
Mas essa é a resposta?
Nãooo, ainda falta olhar a componente da aceleração no sentido tangencial.
A Aceleração Tangencial é responsável por mudar o módulo da velocidade. Se ela estiver no mesmo sentido da velocidade, aumenta, mas se estiver no sentido contrário da velocidade, diminui.
Então, haverá uma componente tangencial apenas no ponto A e C, pois a velocidade está aumentando e diminuindo, respectivamente:
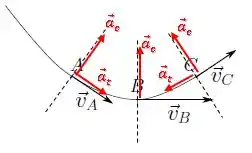
Já no ponto B, não há aceleração tangencial pois sua velocidade não está aumentando nem diminuindo, já que ele está no ponto mínimo de altura da trajetória.
Então, somando os vetores em A e B, temos que nossos vetores resultantes da aceleração serão esses aqui (em azul):
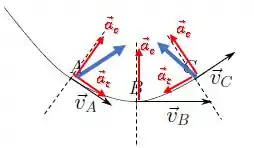
Ficamos com a alternativa (a).
Resposta
Letra (a)