USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I -Cinemática, Leis de Newton, Trabalho e Energia, Questão 33
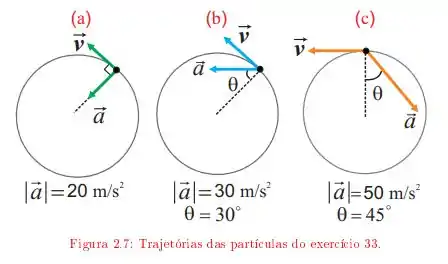
Na figura podemos observar o movimento de três partículas, num certo instante . Todas elas deslocam-se no sentido anti-horário sobre círculos de raio , com velocidades variáveis (direção e/ou módulo). Nestes instantes aparecem, indicados nas figuras, também os vetores aceleração e seus módulos. Em cada um dos instantes assinalados na figura, achar os vetores velocidade e aceleração.
Passo 1
Eaew, belezinha?
Temos três partículas em movimentos circulares de raio , com a posição em um instante como indicado na figura
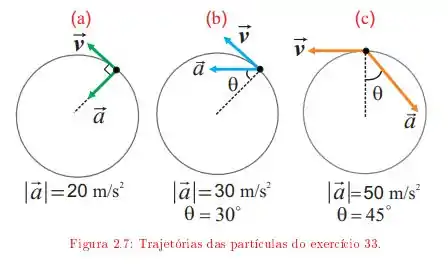
Para cada situação nos foi dada a aceleração e o ângulo entre a aceleração e a direção radial! Vamos usar isso para achar ambos os componentes do vetores aceleração
e o módulo da velocidade pode ser obtido utilizando que
Vamos tentar fazer isso!
Passo 2
Na situação temos que o vetor aceleração é totalmente radial, portanto, podemos afirmar que
e, portanto, o módulo da velocidade é tal que
E, portanto a velocidade é
Ou seja, podemos resumir a situação como
e
Vamos para a próxima situação!
Passo 3
Na situação temos que a componente radial é dada por
ou simplesmente
analogamente, temos a componente tangencial como
de forma que
Usando a aceleração centrípeta obtida podemos calcular o módulo da velocidade como
de forma que o vetor velocidade é
Resumindo, para esta situação temos que
Vamos para a próxima agora!
Passo 4
Finalmente a última situação pode ser resolvida analogamente, temos que
finalmente, obtemos que
e, a parte tangencial é
finalmente temos a velocidade como
sendo assim o vetor velocidade é
e, a aceleração é tal
A questão foi isso! Te vejo na próxima! Tchau Tchau!