Uma partícula descreve um movimento de trajetória circular de raio . A aceleração dessa partícula é dada por , onde é uma constante positiva, a velocidade angular varia com o tempo e os vetores e são os unitários nas direções radial e tangencial ao movimento. Qual a única incorreta das frases a seguir?
(a) O módulo da velocidade linear é constante durante o movimento.
(b) O vetor velocidade é sempre perpendicular ao vetor posição.
(c) A partícula leva cada vez menos tempo para dar uma volta completa no círculo definido pela sua trajetória.
(d) O vetor velocidade não é perpendicular ao vetor aceleração.
Passo 1
A partícula descreve um movimento circular, okay.
A aceleração desse movimento circular é .

Calma, vamos tentar entender pra onde aponta essa aceleração.
A aceleração apresenta duas componentes. Uma delas está na direção , que é um vetor unitário na direção de um eixo radial ao movimento:
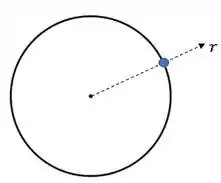
Esse eixo aponta sempre do centro para a posição da partícula.
Então, se a componente nessa direção é negativa, ele apresenta uma aceleração de módulo apontando para o centro do círculo:
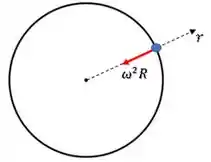
Que apresenta o mesmo módulo de uma força centrípeta:
Afinal, a partícula realiza um movimento circular, certo?
A segunda componente está na direção , que representa a direção tangencial ao movimento:
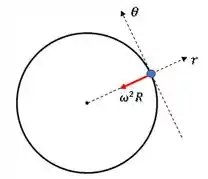
Então, a partícula também sofre uma aceleração tangencial ao movimento de módulo :
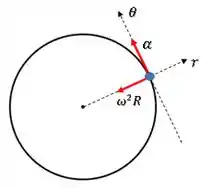
Ahhh, agora ficou mais fácil de entender o que está acontecendo.
Então, vamos analisar as alternativas.
Passo 2
(a) O módulo da velocidade linear é constante durante o movimento.
Se a partícula sofresse apenas a componente da aceleração que aponta para o centro da trajetória circular (aceleração centrípeta), ela estaria realizando um movimento circular uniforme e o módulo da sua velocidade linear seria constante.
Porém, a partícula apresenta uma aceleração tangencial, ou seja, sua velocidade linear assim como sua velocidade angular mudarão.
A letra (a) é falsa, logo, já achamos a incorreta.
Mas vamos dar uma olhada nas outras, porque não né? hahah
Passo 3
(b) O vetor velocidade é sempre perpendicular ao vetor posição.
Como a partícula descreve uma trajetória circular, sua velocidade é sempre perpendicular à sua posição:
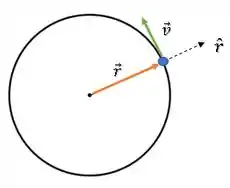
A letra (b) está correta.
Passo 4
(c) A partícula leva cada vez menos tempo para dar uma volta completa no círculo definido pela sua trajetória.
Se a partícula tem uma aceleração tangencial, sua velocidade vai aumentando. Logo, a partícula vai percorrer o mesmo trajeto mais rapidamente, portanto, o tempo de uma volta será cada vez menor.
A letra (c) está correta.
Passo 5
(d) O vetor velocidade não é perpendicular ao vetor aceleração.
O vetor aceleração será a soma daquelas duas componentes:
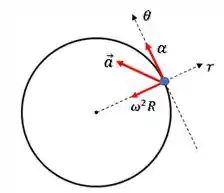
Enquanto isso, sua velocidade é tagencial ao círculo:
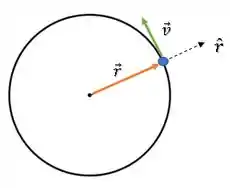
Portanto, eles realmente não serão perpendiculares.
A letra (d) está correta.
Resposta
Letra (a)