Dois carros percorrem uma pista de corrida circular no mesmo sentido. O carro A viaja com rapidez constante de . O carro B parte do repouso e sua rapidez cresce a uma taxa constante até atingir . Quando o carro B tem a mesma rapidez que o carro A, é sempre verdade que:
(A) o carro B está ultrapassando o carro A.
(B) o carro B tem mesma aceleração tangencial que o carro A.
(C) o carro B tem mesma aceleração radial que o carro A.
(D) o carro B tem mesma aceleração que o carro A.
(E) o carro B percorreu uma distância maior do que A.
Passo 1
Como os carros A e B percorrem uma pisca de corrida circular, ambos estão sempre à mesma distância do centro da pista (raio).
No instante em que as velocidades de A e B possuem o mesmo valor, temos, por exemplo, o seguinte cenário:
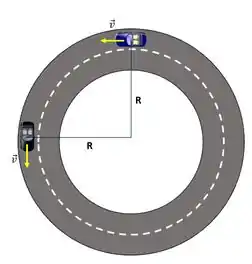
Lembrando da relação da força centrípeta, temos:
Logo, a aceleração radial é dada por:
Como no instante analisado ambos os carros possuem mesma velocidade e mesmo raio, podemos dizer que a aceleração radial é a mesma para os dois.