Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Não-Ideais

Ver Teoria
Exercício 2912345678910111213141516171819202122232425262728303132333435363738394041424344454647

Enunciado

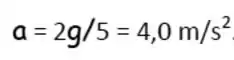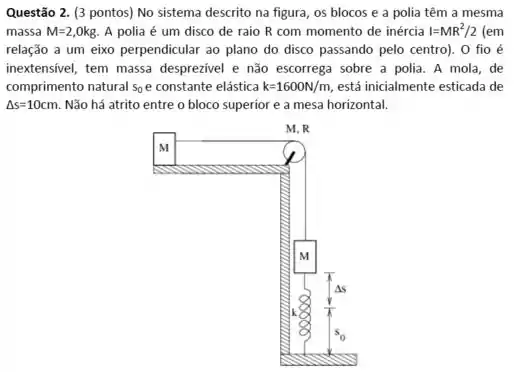
Passo 1

Aqui vamos usar sempre a mesma justificativa, a energia se conserva porque não há ação de forças externas e nem atrito cinética no sistema blocos + polias + terra + mola

Passo 2

Usando o que já descobrimos com a l e t r a   a , vamos conservar a energia mecânica nos pontos para descobrir as velocidades.

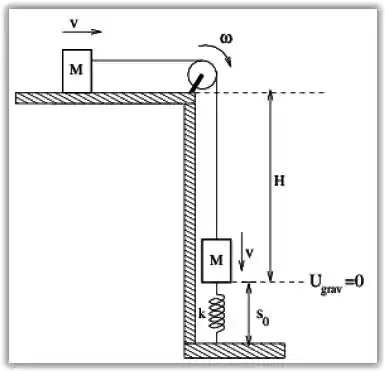
Como os blocos estão ligados pelo mesmo fio, a velocidade de ambos tem que ser a mesma.

m v 2 2 + m v 2 2 + I ω 2 2 + m g h = m g ∆ S + k ∆ s 2 2 + m g h

Como o bloco não muda de posição em relação a horizontal, podemos sumir com esse m g h .

Outra alteração que devemos fazer também é substituir as seguintes expressões

I = M R 2 2

ω = v R

Trocando tudo que a gente precisa ficamos com a expressão

2 m v 2 + m v 2 2 = 2 m g ∆ S + k ∆ s 2

Substituindo os valores que foram dados no enunciado temos

m = 2,0   k g

∆ s = 0,1 m

k = 1600   N / m

g = 10   m / s 2

2   x   2   x   v 2 + 2   x   v 2 2 = 2   x   2   x   10   x   0,1 + 1600     x   0,1 2

v = 2,0   m / s

Passo 3

O que vamos fazer nessa questão é escrever uma equação pra cada objeto, pra depois descobrirmos a aceleração de cada bloco.

Antes de começarmos, podemos pensar que a aceleração linear de todo o sistema precisa ser igual, porque todos eles estão ligados por um mesmo fio

A força que a mola vai exercer também podemos considerar ela nula, porque como ela vai estar em seu comprimento natural não vai exercer força nenhuma.

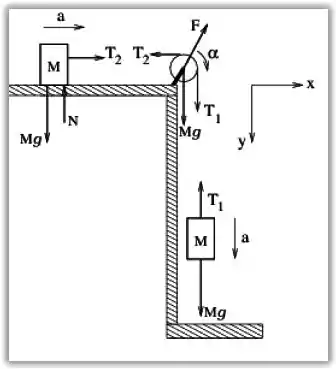
Pro bloco superior temos

M a = T 2

Bloco inferior temos

M a = M g - T 1

Polia, sentido horário

I α = T 1 R - T 2 R

Agora fazendo aquelas substituições manjadas que a gente já sabe

a = α R

I = M R 2 2

Ficamos assim

M a 2 = T 1 - T 2

Somando as primeiras equações com essas ultimas pra podermos sumir com as trações e ficarmos só com as acelerações temos

5 M a 2 = M g

a = 4,0   m / s 2

Resposta

Exercícios de Livros Relacionados

Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,