Um elevador pode ser representado esquematicamente como um bloco de massa para indicar a cabine (caixa de metal + carga), um bloco de massa representa um contra-peso para a cabine e uma polia de raio cujo momento de inércia é . Um motor está acoplado a polia e pode realizar um torque para tracionar os cabos (considerados ideais). O módulo da tração sobre a massa é , enquanto é a tração sobre . Considere que os cabos não deslizam sobre a polia e utilize .
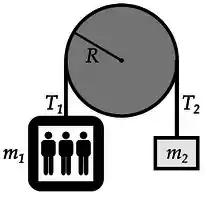
(a) Represente diagramaticamente todas as forças que atuam sobre as massas e e os torques sobre a polia.
(b) Escreva a segunda lei de Newton as massas , e a polia em termos da aceleração a da massa .
(c) Considere que a polia move-se com velocidade angular constante, de módulo . Qual é o módulo da potência que deve ser aplicada ao motor?
Passo 1
Na letra (a), queremos o diagrama de forças sobre os corpos.
Elevador:
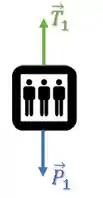
Contra-Peso:
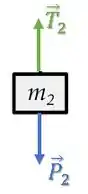
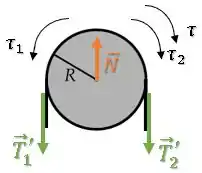
Roldana:
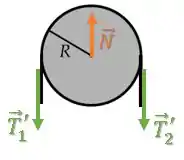
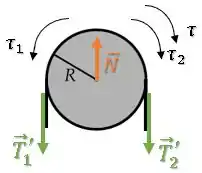
Sobre a roldana, existem uma força de tração de cada lado puxando-a para baixo.
Essas forças de tração apresentam o mesmo módulo de e , porém, representamos como e pois os vetores apontam em direção diferente dos vetores e :
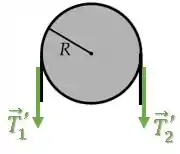
Para evitar que essa roldana seja puxada para baixo, temos uma força normal para cima:
Além disso, a questão pede para respresentar os torques sobre a roldana.
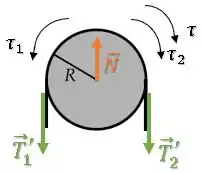
A força não gera torque, pois está aplicada no centro de rotação da roldana.
A força gera um torque no sentido anti-horário, enquanto gera um torque no sentido horário.
Fora esses, ainda temos um torque do motor sobre a roldana que tenta fazer o elevador subir, girando no sentido horário:
Passo 2
Na letra (b), queremos a segunda lei de Newton para cada corpo.
Devemos prestar atenção no sentido da aceleração (cima ou baixo).
Além disso, como o cabo é inextensível, o movimento do contra-peso e do elevador acontecem exatamente com um mesmo deslocamento, velocidade e aceleração. Por isso:
Para o elevador,
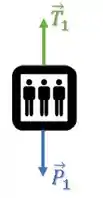
como ele está subindo, sua aceleração é para cima:
Para o contra-peso,
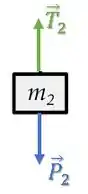
Como ele está descendo, sua aceleração é para baixo. Vamos considerar esse sentido positivo:
Passo 3
Já na roldana, não há translação, existe apenas rotação.
Logo, vamos aplicar a segunda Lei de Newton para rotação:
Como está aplicada no centro de rotação, seu torque é nulo.
Tanto a força quanto a força estão perpendiculares aos vetores posição :
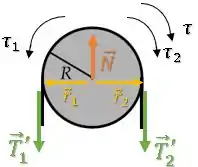
Então os módulos dos torques são:
Mas não podemos nos esquecer do sinal dos torques.
Se a roldana gira no sentido horário, o sentido positivo de sua aceleração angular será no sentido horário, então:
Lembrando que os módulos da força de tração são iguais em cada lado da corda:
Mas antes de respondermos, existe mais um detalhe...
Passo 4
A expressão deve estar em função da aceleração .
Como não há delizamento, a aceleração de um ponto da borda da polia será a mesma aceleração da corda e consequentemente dos blocos .
Podemos relacioná-las com:
Substituindo na expressão da Segunda Lei de Newton para a roldana, temos:
Respondemos a letra (b).
Passo 5
Na letra (c), queremos a potência do motor se a velocidade angular da polia for .
Beleza, mas como que achamos a potência do motor??
Vamos calcular usando a expressão:
Ué... mas de onde vem isso?
Bom, existem umas manipulações a partir da equação de potência que chegam a isso.
Lembrando que é com a prática que você começaria a enxergar isso. Pra quem nunca viu dessa forma, realmente é mais difícil advinhar essas manipulações.
Vamos lá!
Sabemos que o trabalho é o produto entre uma força e um deslocamento :
Agora, vamos usar uma malandragem de multiplicar em cima e em baixo pelo raio :
O primeiro produto é igual a torque e o segundo é igual a :
Passo 6
Já temos o nosso , basta achar o .
Bom, se a velocidade é constante, não há aceleração no sistema.
Ou seja, tanto a roldana, quanto o elevador, quanto o contra-peso se movem sem aceleração.
Então, nossas equações ficam assim.
Elevador:
Contra-peso:
Roldana:
Juntando tudo:
Passo 7
Substituindo a primeira e segunda equações na terceira, temos:
Substituindo os valores, temos:
Passo 8
Agora, podemos calcular a potência para uma velocidade angular de .
Resposta
(a)
Elevador:
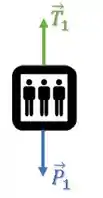
Contra-Peso:
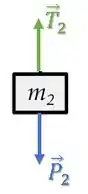
Roldana:
(b)
(c)