Uma roldana com de raio está montada num eixo horizontal sem atrito. O momento de inércia da roldana em relação ao eixo de rotação é . Uma corda de massa desprezível está enrolada na roldana e presa a um bloco de que desliza sobre uma superfície horizontal sem atrito. A corda não desliza em relação à roldana. Se uma força horizontal de módulo é aplicada ao bloco, qual é o módulo da aceleração angular da roldana?
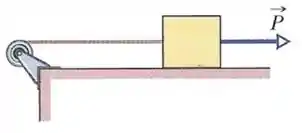
(A)
(B)
(C)
(D)
(E)
Passo 1
Temos que no fio há uma tensão de forma que a segunda lei de Newton para o bloco fica
Passo 2
Só que essa tensão faz um torque sobre a roldana. Como a tensão é horizontal e a linha que conecta o eixo de rotação da roldana e o ponto de contato com a corda é vertical temos que o torque exercido pela tensão da corda é dado por
Onde é o raio da roldana.
Temos o torque se relaciona com a aceleração angular por
Assim
Passo 3
A última coisa que precisamos é a relação entre a aceleração angular e a aceleração linear do fio. Como o fio não desliza e o tanto que o bloco anda o fio também se desloca temos que a aceleração linear do bloco se relaciona com a aceleração angular da roldana por
Assim voltando para
Colocando em evidência, temos:
Substituindo os valores:
Resposta
(B)