Uma máquina de Atwood possui massas , e uma polia maciça uniforme de massa M =2,0kg. O módulo da aceleração linear da massa vale:
a)
b)
c)
d)
e)
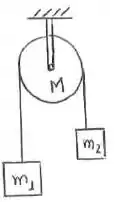
Passo 1
Isolando as forças, teremos:
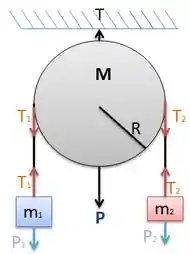
Passo 2
Assumindo que o bloco de massa está descendo e utilizando a segunda Lei de Newton para esse bloco, teremos:
Para o bloco de massa , teremos:
Passo 3
Calculando a Segunda Lei de Newton para rotação, teremos:
Obs: E ah! O como consideramos a aceleração positiva para baixo, devemos considerar o nosso positivo no sentido anti-horário
O torque total sobre a polia é dado por
Passo 4
O da polia é dado por e a aceleração angular é dada por .
Assim:
Passo 5
Agora pegando a equação de Newton do bloco de massa e substraindo da equação do bloco , teremos:
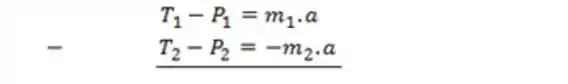
Mas daí,do Passo 3 nós sabemos que . Substituindo aqui, teremos:
Isolando o , vai ficar...
Passo 6
Substituindo de vez agora os valores, teremos:
Resposta
Letra D