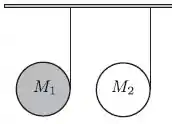
Dois discos de mesmo raio e de massa diferentes, onde , estão presos ao teto por fios ideais e enrolados em suas bordas. Liberados a partir do repouso eles caem verticalmente onde é o módulo da aceleração local da gravidade; o momento de inércia de um disco em torno do seu eixo de rotação que passa pelo seu centro é igual . Os módulos das trações nos fios em cada disco são e e as acelerações dos seus centros de massa são e , respectivamente, a opção correta abaixo é:
- ;
- e
Passo 1
Quando os discos caem eles descem verticalmente, isso quer dizer que eles rodam em torno do seu centro.
A única força que atua no disco fazendo torque é a tração, fazendo ele girar no sentido anti-horário
O enunciado disse o momento de inércia do disco, então
Lembrando que, nesse caso
Resultando em
Passo 2
Além disso as forças que atuam no disco, que são o peso e a tração vão ter a seguinte equação
O sinal da aceleração é importante para termos compatibilidade de movimentos, já que o disco roda no sentido anti-horário a aceleração é para baixo.
Substituindo o que achamos no passo 1
Então
Repara que eu fiz essa conta toda para um disco qualquer, por isso não disse se era ou . A aceleração não depende da massa, então elas são iguais
Resposta
Letra C