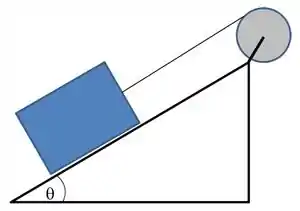
Um cabo ideal está enrolado em volta de uma polia de raio e massa e tem sua outra extremidade ligada a um bloco de . O bloco se encontra apoiado sobre um plano inclinado de em relação a horizontal. O sistema é solto a partir do repouso. Não existe atrito entre o plano e o bloco. Considerando o momento de inércia da polia , calcule:
A aceleração angular da polia.
a tração no cabo e o torque na polia.
O módulo da aceleração linear de um ponto na borda na polia após de iniciado o movimento.
Passo 1
Para descobrir a aceleração angular da polia, devemos utilizar a fórmula do torque, onde .
No entanto, precisaremos de mais uma equação. Como existe um vínculo entre os dois corpos, podemos também usar , pois sabemos que .
Se liga nas equações:
Passo 2
Agora que já temos em função de , vamos à equação para o bloco:
Substituindo na equação, temos:
A aceleração angular fica:
Passo 3
Ahh...fazer esse item ficou fácil depois de ter feito o anterior! Queremos saber a tração , que a gente ja deixou em função de e de , lembra?!
Agora que a gente já tem o valor de , ficou fácil!
Já o torque da polia é dado por:
Passo 4
Para achar a aceleração linear, temos que achar a aceleração tangencial e a aceleração centrípeta, que são as componentes da aceleração linear. Lembra?! Vamos começar pela tangencial, a gente já calculou no item , mas vamos lá!
Agora vamos achar a centrípeta.
Sabemos que depois de , temos:
Então a aceleração centrípeta fica:
Passo 5
Agora que temos a aceleração tangencial e a aceleração centrípeta, basta fazer aquele Pitágoras básico para achar a aceleração linear! Olha só!
Resposta
;