Dois blocos de massas e , com estão ligados por uma corda de massa desprezível que passa, sem deslizar, por uma polia de massa e raio , como mostrado na figura. A polia gira sem atrito sobre um eixo que atravessa seu centro de massa. Julgue as afirmações abaixo:
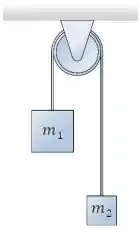
() O módulo da tração exercida pela corda sobre o bloco 1 é igual ao módulo da tração exercida pela corda no bloco 2.
() O módulo da tração exercida pela corda sobre o bloco 1 é maior que o módulo da tração exercida pela corda sobre o bloco 2.
() A aceleração angular da polia é diretamente proporcional à diferença entre as trações exercidas pela corda nos blocos 1 e 2.
Qual opção abaixo contém todas as afirmações que estão corretas?
(A)
(B)
(C) e
(D) e
(E) e
Passo 1
Se a massa é maior que , o bloco 1 vai descer puxando o bloco 2 para cima:
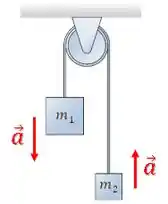
Então, a polia vai girar no sentido anti-horário.
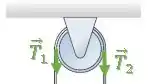
Agora, vamos olhar as forças de tração sobre a corda em cada um dos lados:
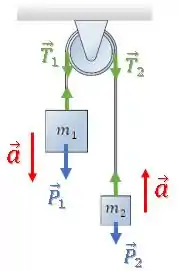
Olhando só para a polia, temos:
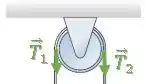
As únicas forças que geram torque na polia são as forças de tração e . Se a polia deve girar no sentido anti-horário, o torque nesse sentido deve ser maior que no sentido horário.
Como a força é responsável pelo torque no sentido anti-horário, temos que essa força deve ser maior que a tração :
Então, a afirmativa está incorreta, pois as trações em cada bloco são diferentes.
Já a afirmativa está correta, pois a tração no bloco 1 será maior que a tração no bloco 2.
Porque essas trações são diferentes?
A gente não tinha visto que as trações eram constantes ao longo de um cabo?
Isso era verdade quando trabalhávamos com polias ideais...
Agora, temos uma polia de massa e raio , então, ela também é um corpo extenso que entrará em movimento por meio da força de tração.
A polia não irá transladar, porém, ela irá entrar em rotação e isso demanda uma certa força gerando um torque nela.
A ideia, entre muitas aspas hahah, é que parte dessa força é ””gasta”” para fazer a polia entrar em rotação, ““sobrando”” uma tração menor para ser aplicada no bloco 2.
Passo 2
Falta analisar a última afirmativa.
Para saber se a aceleração angular da polia é diretamente proporcional à diferença entre as trações exercidas pela corda nos blocos 1 e 2, vamos escrever a segunda lei de Newton para rotação na polia:
Quem são os torques sobre a polia?
Nem está no desenho, porém existem uma força peso e uma força normal aplicadas na polia, entretanto, essas forças não geram torque pois estão aplicadas no centro de rotação da polia.
As únicas forças que geram torque são e :
Como essas forças são perpendiculares ao vetor que liga o centro de rotação ao ponto de aplicação da força:
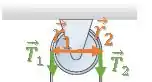
Os módulos dos torques serão dados pela força multiplicados pelo raio da polia. Porém, cada uma tenta fazer a polia girar em um sentido diferente, portanto, seus torques terão sinais opostos:
Isolando , temos:
Assim, realmente a aceleração angular é proporcional à diferença dos módulos dos torques.
A afirmativa está correta.
Como apenas as afirmativas e estão corretas, ficamos com a letra (E).
Resposta
Letra (E)